Describing Oscillations
- An oscillation is defined as follows:
The repetitive variation with time t of the displacement x of an object about the equilibrium position (x = 0)

A pendulum oscillates between A and B. On a displacement-time graph, the oscillating motion of the pendulum is represented by a wave, with an amplitude equal to x0
- Displacement (x) of a wave is the distance of a point on the wave from its equilibrium position
- It is a vector quantity; it can be positive or negative and it is measured in metres (m)
- Period (T) or time period, is the time interval for one complete repetition and it is measured in seconds (s)
- If the oscillations have a constant period, they are said to be isochronous

Diagram showing the time period of a wave
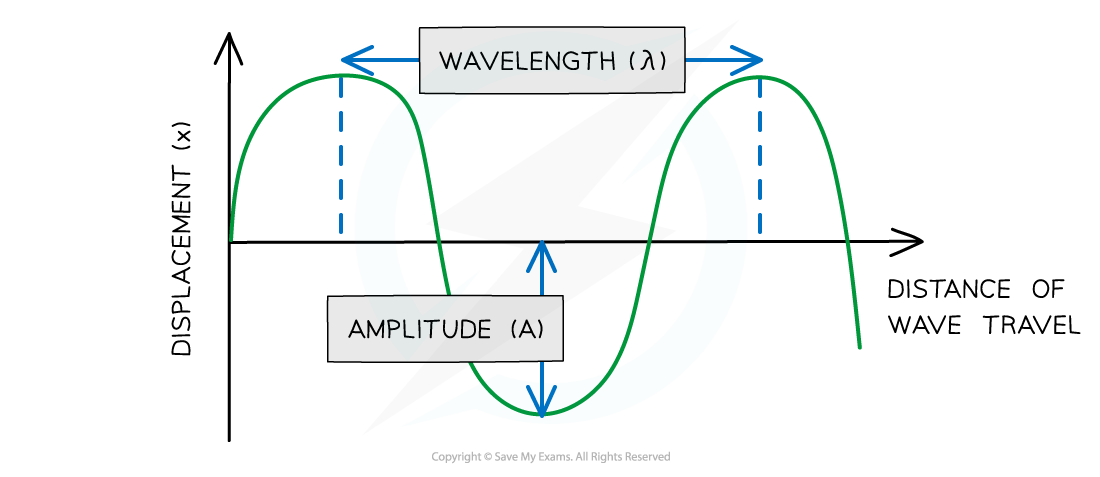
- Amplitude (x0) is the maximum value of the displacement on either side of the equilibrium position is known as the amplitude of the oscillation
- Amplitude is measured in metres (m)
- Wavelength (λ) is the length of one complete oscillation measured from the same point on two consecutive waves
- Wavelength is measured in metres (m)
- Frequency (f) is the number of oscillations per second and it is measured in hertz (Hz)
- Hz have the SI units of per second s−1
- The frequency and the period of the oscillations are related by the following equation:

Phase & Phase Difference
- Phase is a useful way to think about waves
- The phase of a wave can be considered in terms of:
- Wavelength
- Degrees
- Radians
- One complete oscillation is:
- 1 wavelength
- 360°
- 2π radians

Wavelength λ and amplitude A of a travelling wave
- The phase difference between two waves is a measure of how much a point or a wave is in front or behind another
- This can be found from the relative position of the crests or troughs of two different waves of the same frequency
- When the crests of each wave, or the troughs of each wave are aligned, the waves are in phase
- When the crest of one wave aligns with the trough of another, they are in antiphase
- The diagram below shows the green wave leads the purple wave by ¼ λ
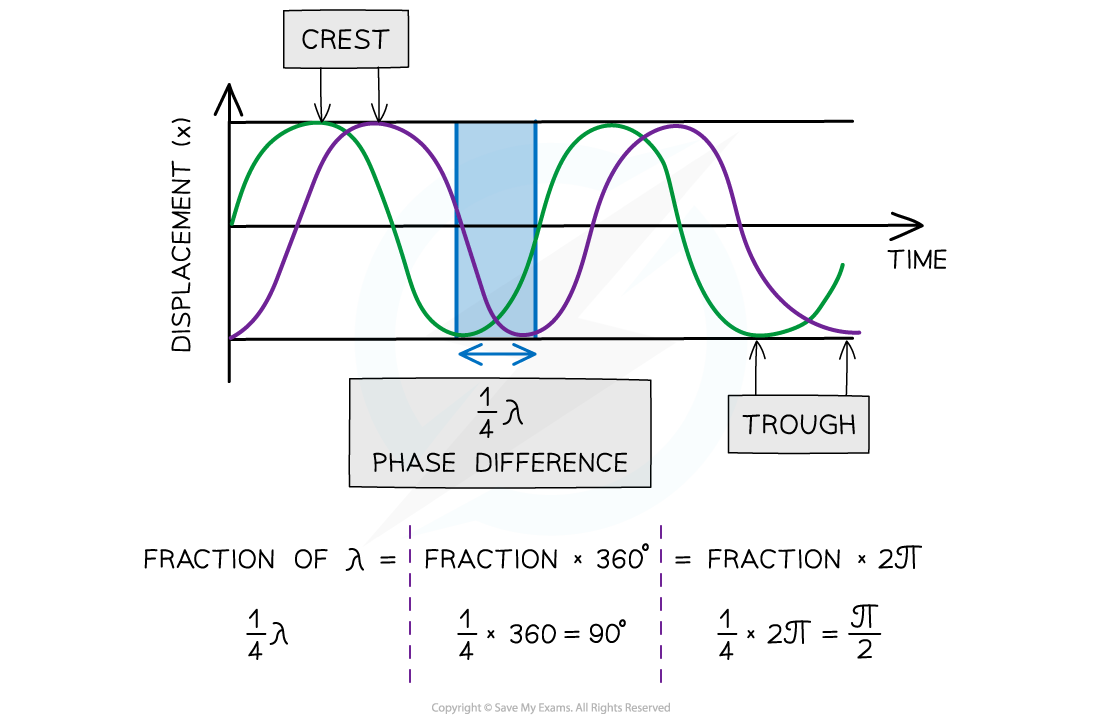
Two waves ¼ λ out of phase
- In contrast, the purple wave is said to lag behind the green wave by ¼ λ
- Phase difference is measured in fractions of a wavelength, degrees or radians
- The phase difference can be calculated from two different points on the same wave or the same point on two different waves
- The phase difference between two points can be described as:
- In phase is 360o or 2π radians
- In anti-phase is 180o or π radians
Worked Example
A child on a swing performs 0.2 oscillations per second.Calculate the period of the child's oscillations.
Step 1: Write down the frequency of the child's oscillations
f = 0.2 Hz
Step 2: Write down the relationship between the period T and the frequency f
![]()
Step 3: Substitute the value of the frequency into the above equation and calculate the period
T = 5 s
Worked Example
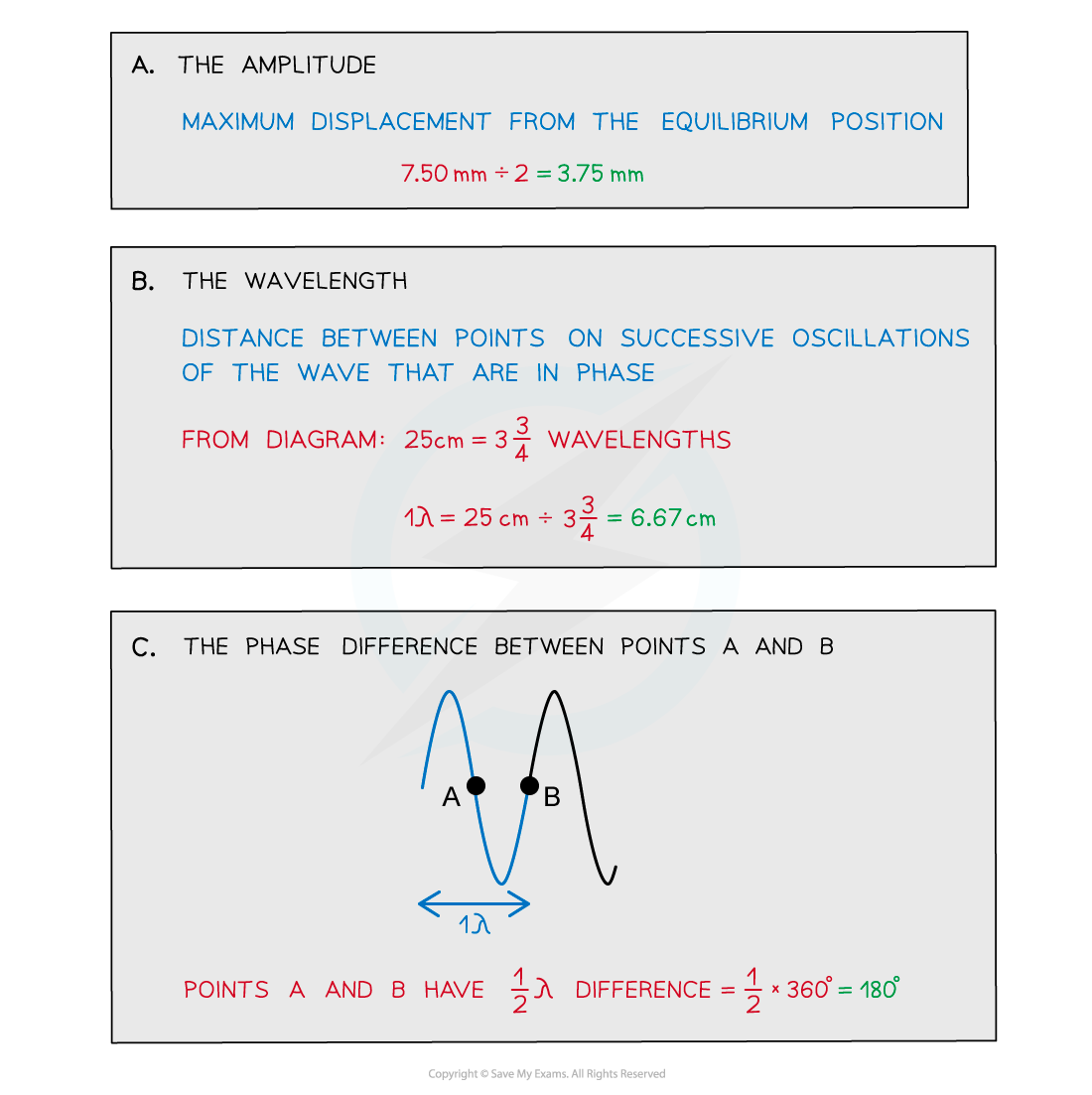
Plane waves on the surface of water at a particular instant are represented by the diagram below. The waves have a frequency of 2.5 Hz.Determine:
The waves have a frequency of 2.5 Hz.Determine:
a) The amplitude
b) The wavelength
c) The phase difference between points A and B
Exam Tip
When labelling the wavelength and time period on a diagram:
- Make sure that your arrows go from the very top of a wave to the very top of the next one
- If your arrow is too short, you will lose marks
- The same goes for labelling amplitude, don’t draw an arrow from the bottom to the top of the wave, this will lose you marks too.
