5.1.2 Drift Speed

• In conductors, only negatively charged (delocalised) electrons are allowed to move between atoms
  • In general, an electric current can arise from the flow of either positive or negative particles
• Charged particles moving through a material or through vacuum are known as charge carriers 

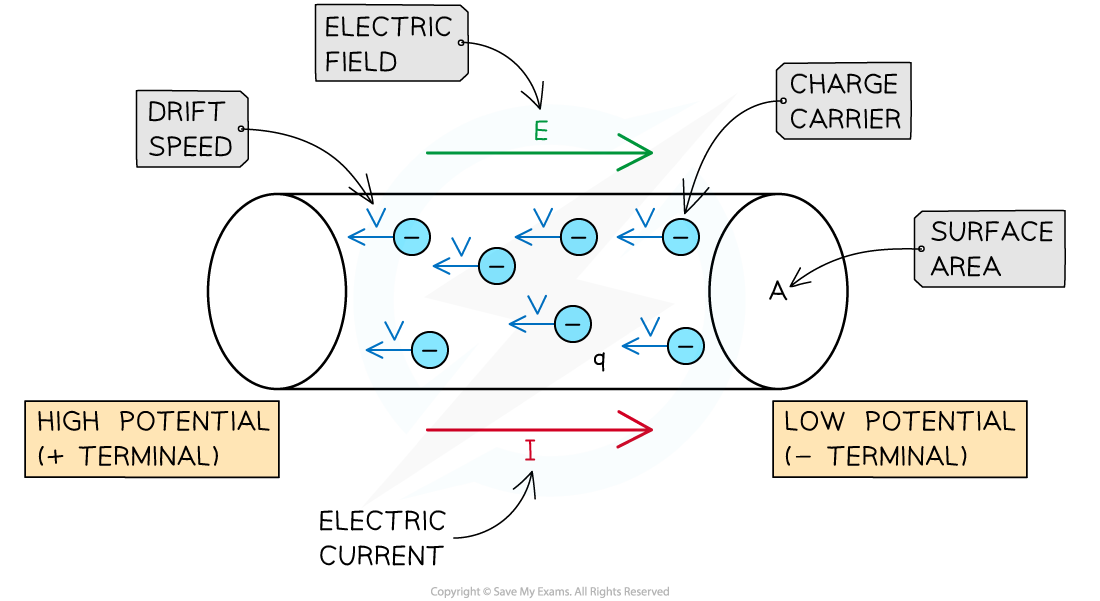
Charge carriers drift towards the positive terminal of the conductor. Conventional current flows in the opposite direction

Movement in a Conductor

• Delocalised electrons are the charge carriers in a conductor
  • These electrons normally move randomly through the conductor

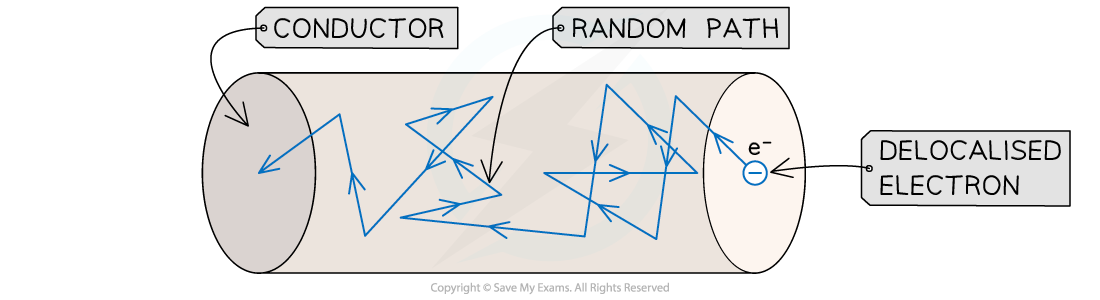
Random path of a delocalised electron through a length of conductor

• If a potential difference is applied between two points in the conductor, an electric field is created
• As a consequence:
  • An electric force will act on the charge carriers
  • The charge carriers will drift along the conductor
  • A steady average current will flow through the conductor

Electric Current & Drift Speed

• The average speed at which the charge carriers move through a conductor is known as the drift speed 
• The value of the drift speed is usually very small
  • For most everyday situations, v ∼ 10^–4 m s^–1

• The electric current arising from the movement of a given number of charge carriers through a conductor is calculated as follows:

I = nAvq

• Where:
  • n = number of charge carriers per unit volume, i.e. charge density (m^–3)
  • A = cross-sectional area of the conductor (m²)
  • v = average drift speed of the charge carriers (m s^–1)
  • q = charge of the charge carriers (C)

Worked Example

Step 1: Write down the equation for electric current 

Step 2: Write down the expression for the total charge Δq and substitute it into the above equation 

• • The total charge is equal to the number of charge carriers times the charge of each carrier

     

• • Substituting this into the current equation:

    

Step 3: Write down the number of charge carriers in terms of charge density n, and substitute it into the above equation 

• • The charge density is equal to the number of charges per unit volume

     

    

• • Substituting this into the current equation:

    

Step 4: Write down the volume of the conductor in terms of cross-sectional area and length, and substitute it into the above equation

• • The volume of the cylindrical section of the conductor is equal to the cross-sectional area times the length

   

• • Substituting this into the current equation:

     

Step 5: Recognise average speed into the above equation 

• • Average speed v is total distance L over total time Δt

• • Substituting this into the current equation