Gravitational Potential Energy
- Gravitational potential energy (Ep) is energy stored in a mass due to its position in a gravitational field
- If a mass is lifted up, it will gain Ep (converted from other forms of energy)
- If a mass falls, it will lose Ep (and be converted to other forms of energy)
- The equation for gravitational potential energy for energy changes in a uniform gravitational field is:
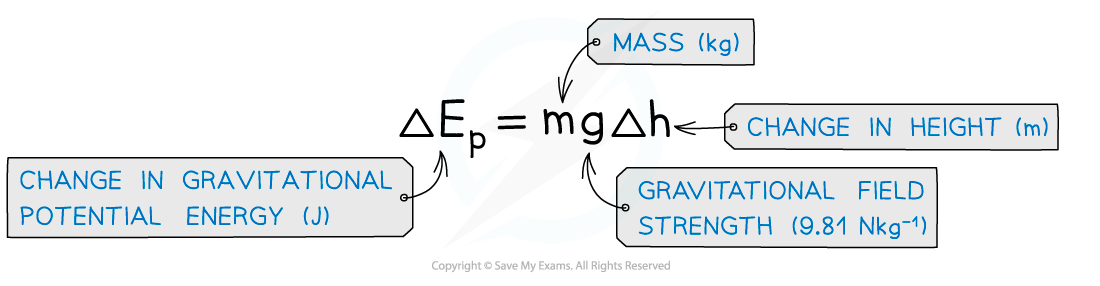
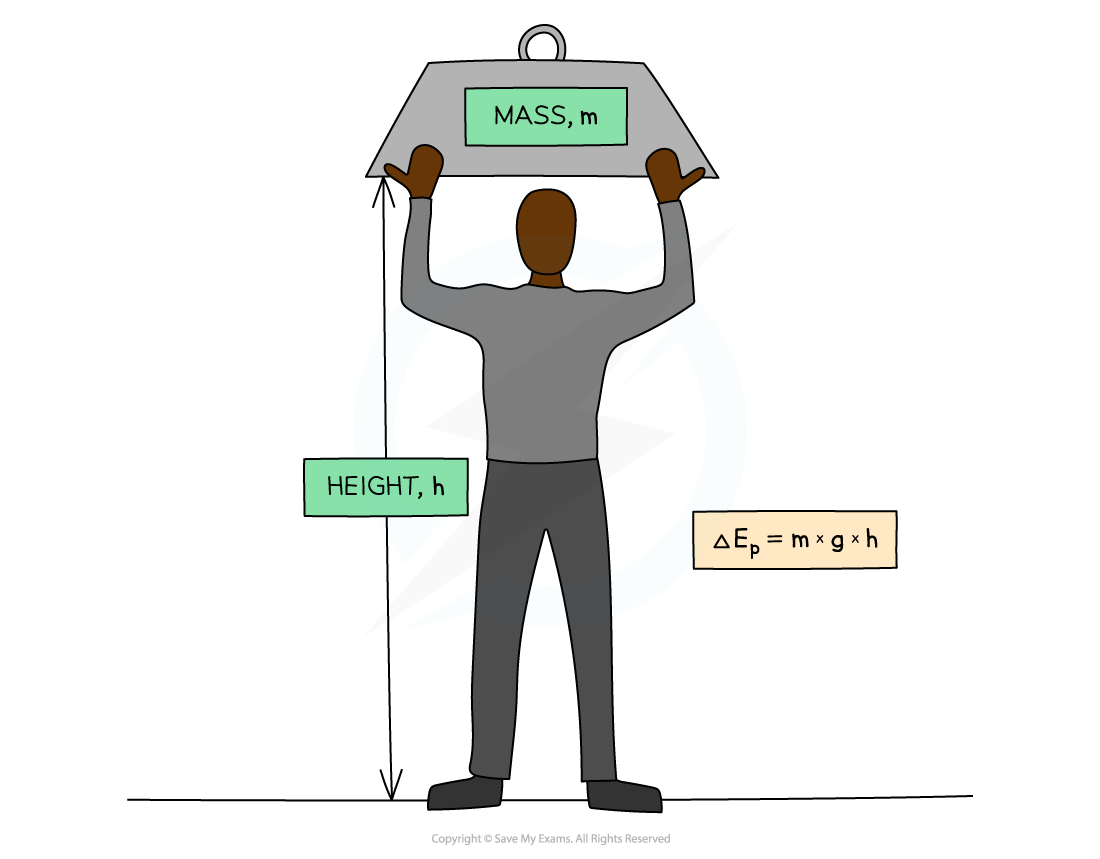
Gravitational potential energy (GPE): The energy an object has when lifted up
- The potential energy on the Earth’s surface at ground level is taken to be equal to 0
- This equation is only relevant for energy changes in a uniform gravitational field (such as near the Earth’s surface)
Derivation of GPE Equation
- When a heavy object is lifted, work is done since the object is provided with an upward force against the downward force of gravity
- Therefore energy is transferred to the object
- This equation can therefore be derived from the work done
Worked Example
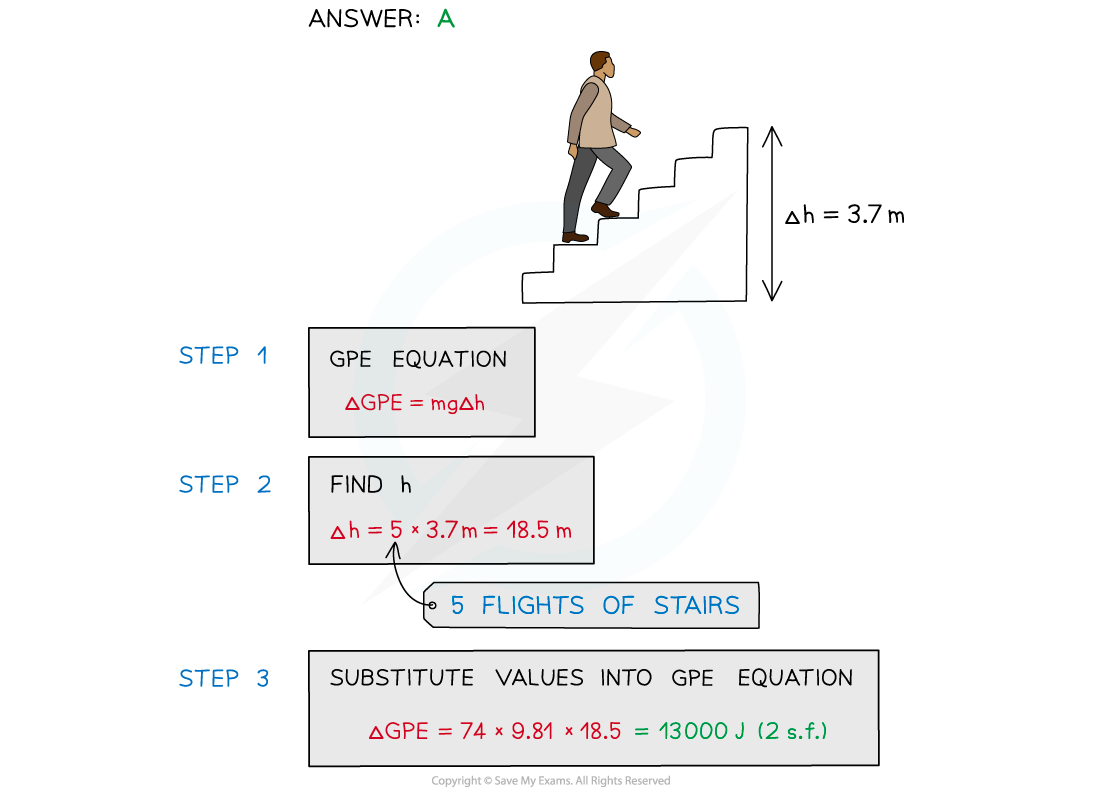
To get to his apartment a man has to climb five flights of stairs.
The height of each flight is 3.7 m and the man has a mass of 74 kg.
What is the approximate gain in the man's gravitational potential energy during the climb?
A. 13 000 J B. 2700 J C. 1500 J D. 12 500 J
GPE vs Height
- The two graphs below show how GPE changes with height for a ball being thrown up in the air and when falling down (ignoring air resistance)
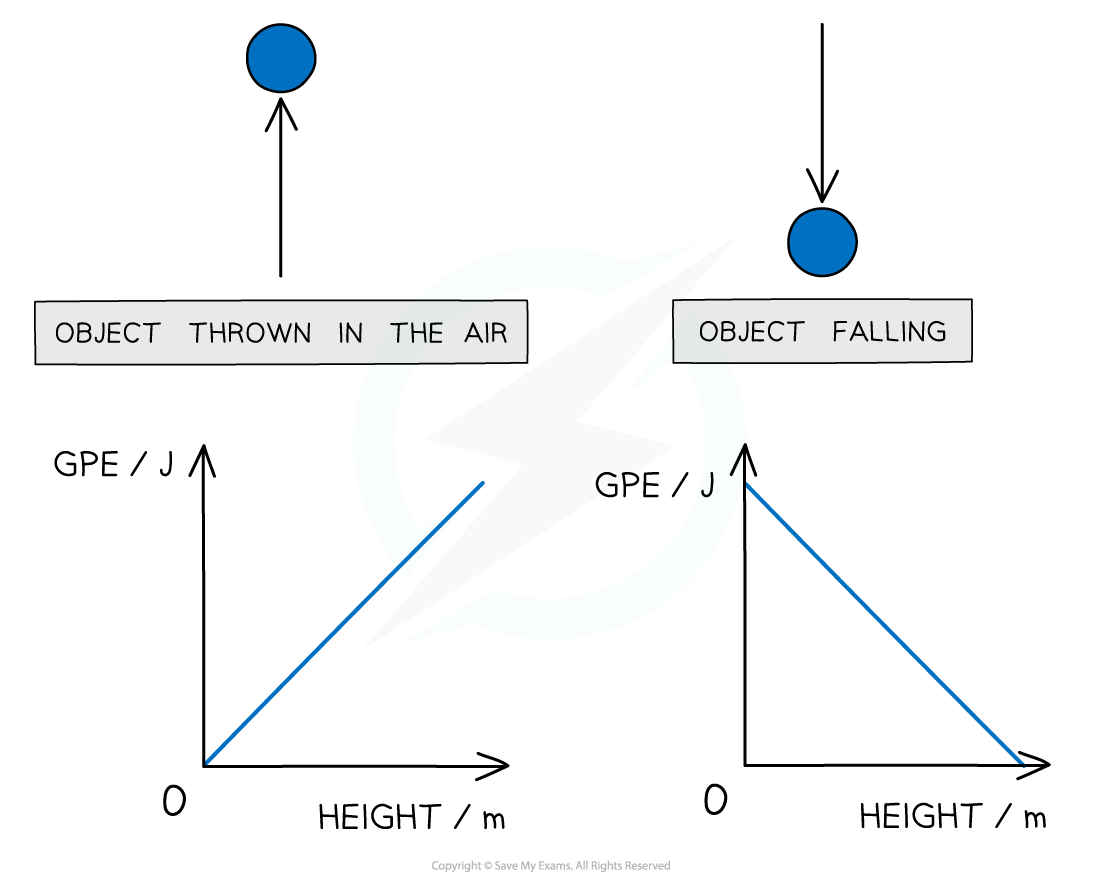
Graphs showing the linear relationship between GPE and height
- Since the graphs are straight lines, GPE and height are said to have a linear relationship
- These graphs would be identical for GPE against time instead of height
Relationship between GPE & KE
- There are many scenarios that involve the transfer of kinetic energy into gravitational potential, or vice versa
- Some examples are:
- A swinging pendulum
- Objects in freefall
- Sports that involve falling, such as skiing and skydiving
- Using the principle of conservation of energy, and taking any drag forces as negligible:
Loss in potential energy = Gain in kinetic energy
Worked Example
The diagram below shows a skier on a slope descending 750 m at an angle of 25° to the horizontal.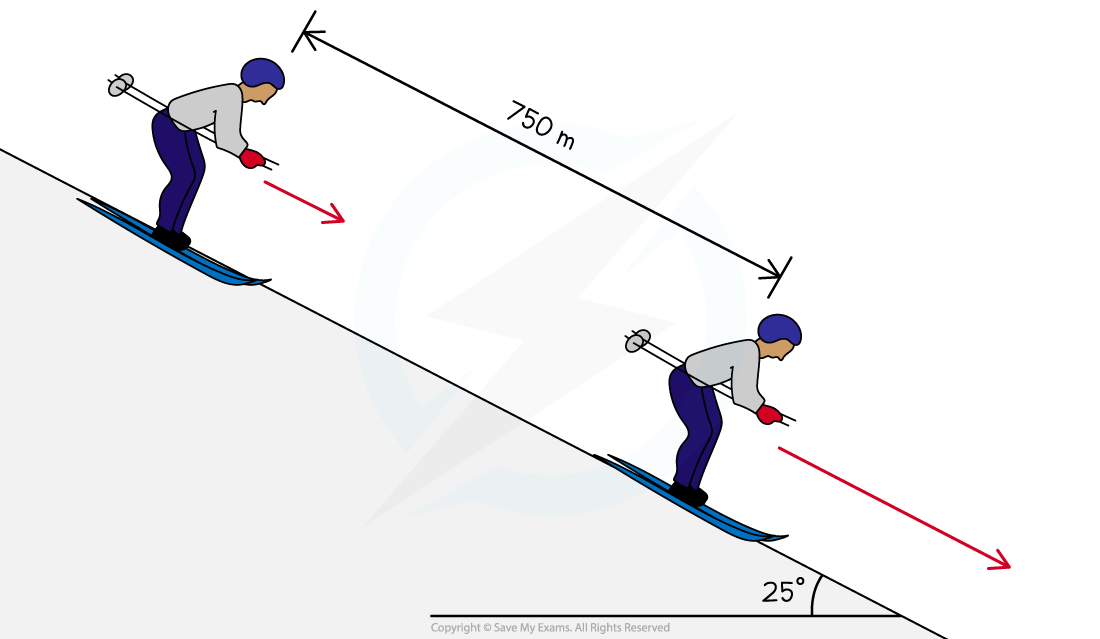
Calculate the final speed of the skier, assuming that he starts from rest and 15% of his initial gravitational potential energy is not transferred to kinetic energy.
Step 1: Write down the known quantities
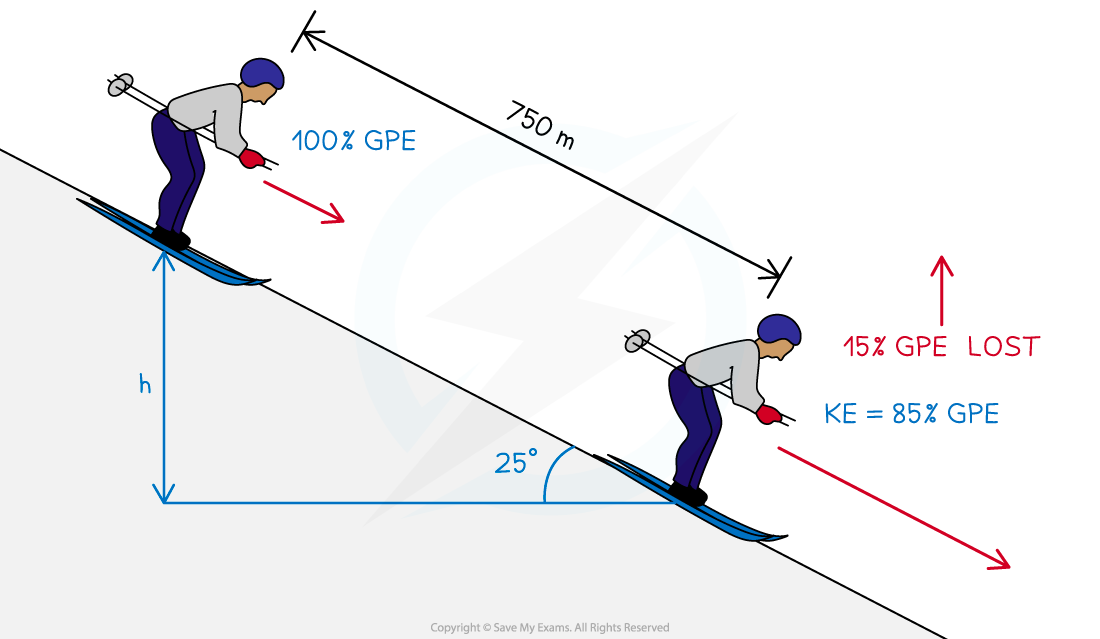
- Vertical height, h = 750 sin 25°
- Ek = 0.85 Ep
Step 2: Equate the equations for Ek and Ep
Ek = 0.85 Ep
½ mv2 = 0.85 × mgh
Step 3: Rearrange for final speed, v
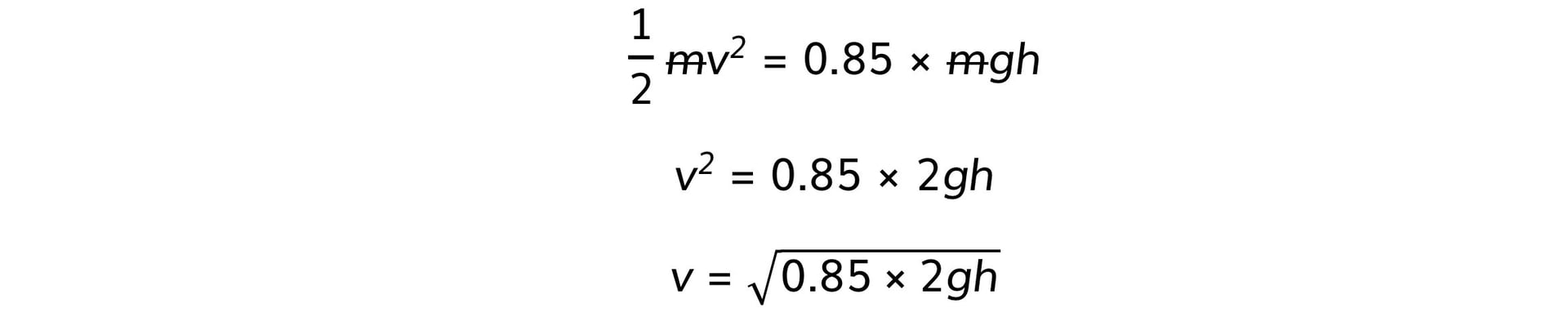
Step 4: Calculate the final speed, v
