Scientific Notation & Metric Multipliers
Scientific Notation
- In physics, measured quantities cover a large range from the very large to the very small
- Scientific notation is a form that is based on powers of 10
- The scientific form must have one digit in front of the decimal place
- Any remaining digits remain behind the decimal place
- The magnitude of the value comes from multiplying by 10n where n is called 'the power'
- This power is positive when representing large numbers or negative when representing small numbers
Worked Example
Express 4 600 000 in scientific notation.
Step 1: Write the convention for scientific notation
-
- To convert into scientific notation, only one digit may remain in front of the decimal point
- Therefore, the scientific notation must be 4.6 × 10n
- The value of n is determined by the number of decimal places that must be moved to return to the original number (i.e. 4 600 000)
- To convert into scientific notation, only one digit may remain in front of the decimal point
Step 2: Identify the number of digits after the 4
-
- In this case, that number is +6
Step 3: Write the final answer in scientific notation
-
- The solution is: 4.6 × 106
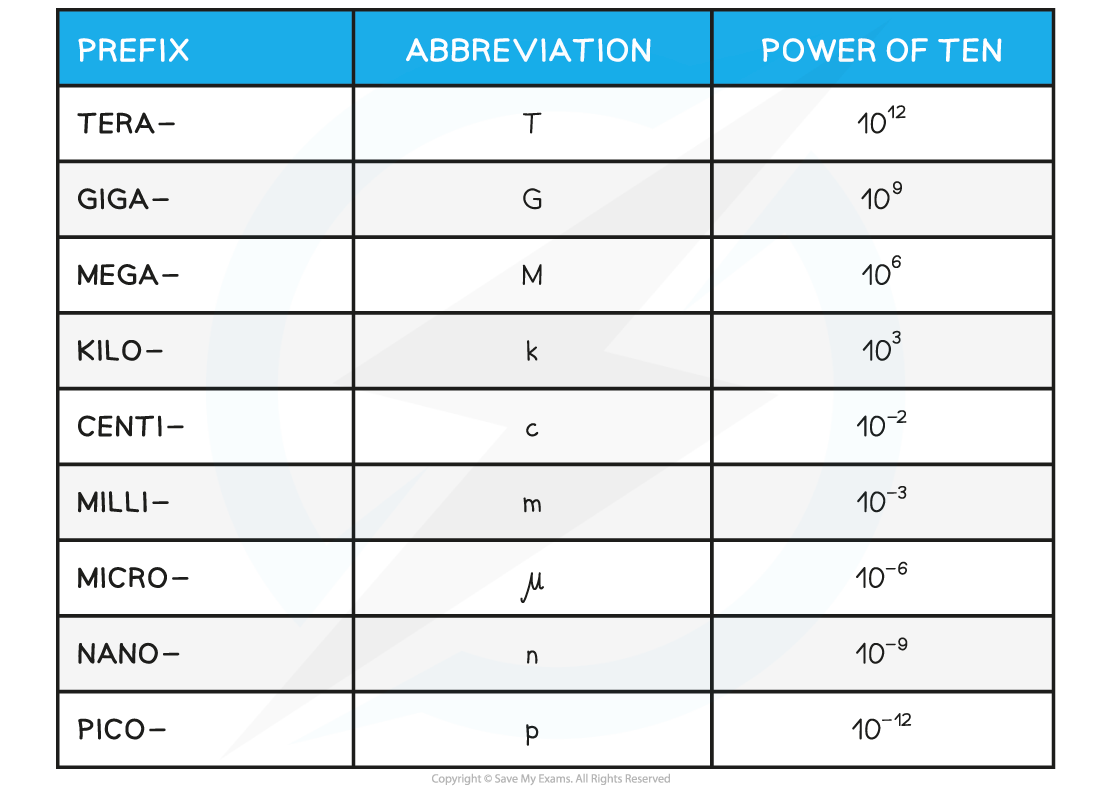
Metric Multipliers
- When dealing with magnitudes of 10, there are metric names for many common quantities
- These are known as metric multipliers and they change the size of the quantity they are applied to
- They are represented by prefixes that go in front of the measurement
- Some common examples that are well-known include
- kilometres, km (× 103)
- centimetres, cm (× 10–2)
- milligrams, mg (× 10–3)
- Metric multipliers are represented by a single letter symbol such as centi- (c) or Giga- (G)
- These letters go in front of the quantity of interest
- For example, centimetres (cm) or Gigawatts (GW)
Common Metric Multipliers Table
Worked Example
What is the answer to the addition of 3.6 Mm + 2700 km in metres?
Step 1: Check which metric multipliers are in this problem
- M represents Mega- which is × 106 (not milli- which is small m!)
- k represents kilo- which is a multiplier of × 103
Step 2: Apply these multipliers to get both quantities to be metres
3.6 × 106 m + 2.7 × 106 m
Step 3: Write the final answer in units of metres
6.3 × 106 m
Exam Tip
You are expected to know metric multipliers for your exams. Make sure you become familiar with them in order to avoid any mistakes.
Significant Figures
- Significant figures are the digits that accurately represent a given quantity
- Significant figures describe the precision with which a quantity is known
- If a quantity has more significant figures then more precise information is known about that quantity
Rules for Significant Figures
- Not all digits that a number may show are significant
- In order to know how many digits in a quantity are significant, these rules can be followed
- Rule 1: In an integer, all digits count as significant if the last digit is non-zero
- Example: 702 has 3 significant figures
- Rule 2: Zeros at the end of an integer do not count as significant
- Example: 705,000 has 3 significant figures
- Rule 3: Zeros in front of an integer do not count as significant
- Example: 0.002309 has 4 significant figures
- Rule 4: Zeros at the end of a number less than zero count as significant, but those in front do not.
- Example: 0.0020300 has 5 significant figures
- Rule 5: Zeros after a decimal point are also significant figures.
- Example: 70.0 has 3 significant figures
- Rule 1: In an integer, all digits count as significant if the last digit is non-zero
- Combinations of numbers must always be to the smallest number significant figures
Worked Example
What is the solution to this problem to the correct number of significant figures: 18 × 384?
Step 1: Identify the smallest number of significant figures
- 18 has only 2 significant figures, while 384 has 3 significant figures
- Therefore, the final answer should be to 2 significant figures
Step 2: Do the calculation with the maximum number of digits
18 × 384 = 6912
Step 3: Round to the final answer to 2 significant figures
6.9 × 103
