3.2.3 Kinetic Model of an Ideal Gas

Gas Pressure

• A gas is made of a large number of particles
• Gas particles have mass and move randomly at high speeds
• Pressure in a gas is due to the collisions of the gas particles with the walls of the container that holds the gas
• When a gas particle hits a wall of the container, it undergoes a change in momentum due to the force exerted by the wall on the particle (as stated by Newton's Second Law)
  
  • Final momentum = –mv
  • Initial momentum = mv
• Therefore, the change in momentum Δp can be written as:

Δp = final momentum – initial momentum

Δp = –mv – mv = –2mv

• According to Newton's Third Law, there is an equal and opposite force exerted by the particle on the wall (i.e. F = 2mv/Δt)

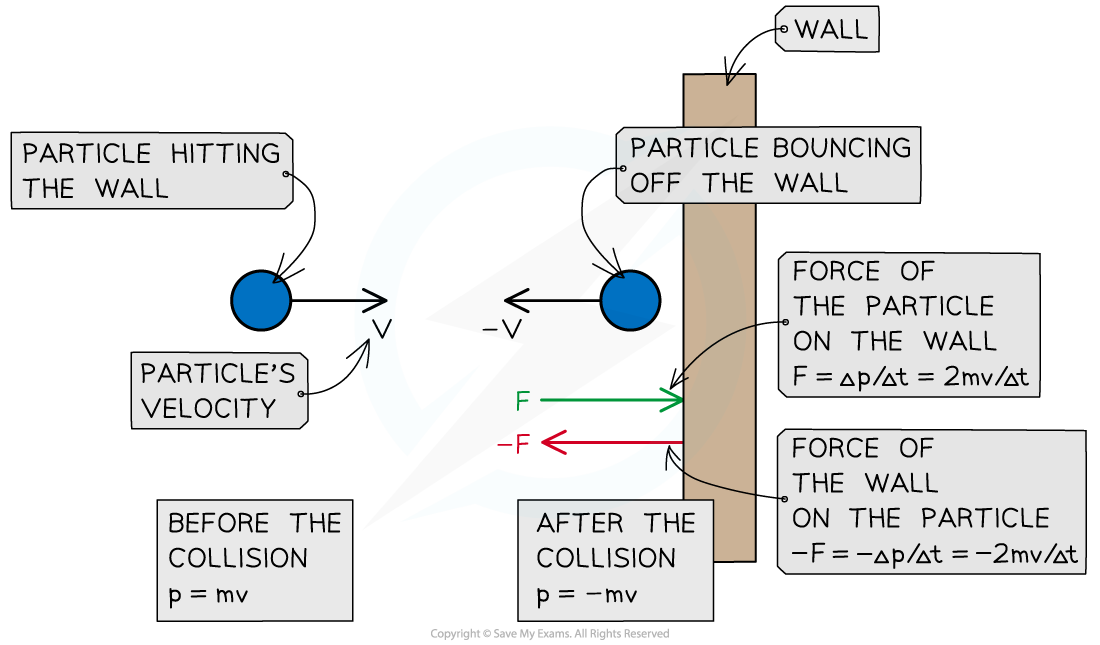
A particle hitting a wall of the container in which the gas is held experiences a force from the wall and a change in momentum. The particle exerts an equal and opposite force on the wall

• Since there is a large number of particles, their collisions with the walls of the container give rise to gas pressure, which is calculated as follows:

• Where:
  • p = pressure in pascals (Pa)
  • F = force in newtons (N)
  • A = area in metres squared (m²)

Average Random Kinetic Energy of Gas Particles

• Particles in gases have a variety of different speeds
• The average random kinetic energy of the particles E_K, which can be written as follows:

• Where:
  • E_K = average random kinetic energy of the particles in joules (J)
  • k_B = 1.38 × 10^–23 J K^–1 (Boltzmann's constant)
  • T = absolute temperature in kelvin (K)

• k_B is known as Boltzmann's constant, and it can be written as follows:

• Where:
  • R = 8.31 J K^–1 mol^–1 (ideal gas constant)
  • N_A = 6.02 × 10²³ mol^–1 (Avogadro constant)

Internal Energy of the Gas

• Using the equation of state of ideal gases, the internal energy can be written as follows:

• Where:
  • U = internal energy of the gas in joules (J)
  • p = gas pressure in pascals (Pa)
  • V = gas volume in metres cubed (m³)

Worked Example

Part (a)

Step 1: Write down the temperature T of the gas in kelvin (K)

T = 47°C = 320 K

Step 2: Write down the equation linking the absolute temperature T of the gas to the average random kinetic energy E_K of the gas particles 

Step 3: Substitute numbers into the equation 

• • From the data booklet, k_B = 1.38 × 10^–23 J K^–1

E_K = 6.6 × 10^–21 J

Part (b)

Step 1: Write down the equation linking the internal energy U of the gas to the number of moles n and the absolute temperature T

Step 2: Substitute numbers into the equation 

• • From the data booklet, R = 8.31 J K^–1 mol^–1

U = 8000 J = 8kJ

• • Note that, alternatively, the internal energy can be calculated using the following equation:

U = NE_K = 8000 J = 8kJ

N = nN_A = 2 mol × (6.02 × 10²³) mol^–1 = 1.2 × 10²⁴

E_K = 6.6 × 10^–21 J (calculated in Step 3)

Exam Tip

• The equation of state of ideal gases and the equations for the kinetic energy of the particles and the internal energy of the gas derived previously, only apply to ideal gases  
• An ideal gas is defined as one to which all the statements below apply:

1. It contains a very large number of identical particles (atoms or molecules)
2. Each gas particle occupies a negligible volume compared to the volume of the gas
   • This means they can be considered as point particles
3. The gas particles move randomly at high speeds 
4. The gas particles obey Newton's laws of motion
5. There are no intermolecular forces between the gas particles
   • Therefore, the internal energy of the gas is equal to the total kinetic energy of the particles (U = NE_K)
6. The gas particles undergo elastic collisions with each other and with the walls of the container in which the gas is held
   • Hence, the total kinetic energy of the particles and the temperature of the gas do not change as a result of these collisions
7. The duration of the collisions is negligible compared with the time interval between collisions
8. Each particle exerts a force on the wall of the container with which it collides
   • This means the average of the forces produced by all gas particles results in a uniform gas pressure 

• Real gases are not ideal gases, however, under certain conditions, they can be considered as ideal gases. An ideal gas is a good approximation of a real gas when:
  • Pressure and density are low
  • Temperature is moderate