DP Mathematics: Applications and Interpretation Questionbank

Write down an equation in $r$ and $h$ that shows this information.

Show that $V=\frac{2500\text{π}h}{3}-\frac{\text{π}{h}^3}{3}$.

Find $\frac{\text{d}V}{\text{d}h}$.

Using your answer to part (c), find the value of $h$ for which $V$ is a maximum.

Find the maximum volume of the bird bath.

To prevent leaks, a sealant is applied to the interior surface of the bird bath.

Find the surface area to be covered by the sealant, given that the bird bath has maximum volume.

Find $\frac{dL}{dx}$

Show that $L=2x+\frac{300}{x}+22$

Find an expression for the total length of the ribbon $L$ in terms of $x$ and $y$.

Hence or otherwise find the minimum length of ribbon required.

Solve $\frac{dL}{dx}=0$

The company regularly increases the number of cars it produces.

Describe how their profit changes if they increase production to over $30$ cars per month and up to $50$ cars per month. Justify your answer.

Find an expression for $P$ in terms of $x$.

Hence find the maximum height of the tunnel.

Hence find the maximum height of the tunnel.

Find $S\prime \left(x\right)$.

Solve $S\text{'}\left(x\right)=0$.

Interpret your answer to (b)(i) in context.

Find the expression $\frac{dV}{d\theta }$.

Solve algebraically $\frac{dV}{d\theta }=0$ to find the value of $\theta$ that will maximize the volume, $V$.

Show that $r=\frac{6}{2+\theta }$.

Find an expression for $V$ in terms of $\theta$.

Find the value of $t$ at which the goat is eating grass at the greatest rate.

Find the value of $t$ at which the goat is eating grass at the greatest rate.

Calculate the surface area of the box in cm².

Find the number of boxes that should be sold each week to maximize the profit.

Find the least number of boxes which must be sold each week in order to make a profit.

Find $P\left(x\right)$.

Calculate the length AG.

Use the model to find how much coffee the cafe should make each morning to maximize its profit.

Show that the volume of the cone may be expressed by $V=\frac{\pi }{3}\left(2R{h}^2-h^3\right)$.

Given that there is one inscribed cone having a maximum volume, show that the volume of this cone is $\frac{32\pi R^3}{81}$.

The graph of $y=f\left(x\right)$ has a local maximum at A. Find the coordinates of A.

Show that there is exactly one point of inflexion, B, on the graph of $y=f\left(x\right)$.

The coordinates of B can be expressed in the form B$\left(2^a,b\times 2^{-3a}\right)$ where a, b$\in \mathbb{Q}$. Find the value of a and the value of b.

Sketch the graph of $y=f\left(x\right)$ showing clearly the position of the points A and B.

Find the area of the window in terms of P and $r$.

Find the width of the window in terms of P when the area is a maximum, justifying that this is a maximum.

Show that in this case the height of the rectangle is equal to the radius of the semicircle.

Consider the curve $y=\frac{1}{1-x}+\frac{4}{x-4}$.

Find the x-coordinates of the points on the curve where the gradient is zero.

Show that there are exactly two points on the curve where the gradient is zero.

Find the equation of the normal to the curve at the point P.

The normal at P cuts the curve again at the point Q. Find the $x$-coordinate of Q.

The shaded region is rotated by 2$\pi$ about the $y$-axis. Find the volume of the solid formed.

Write down the $x$-coordinate of the point of inflexion on the graph of $y=f\left(x\right)$.

find the value of $f\left(1\right)$.

find the value of $f\left(4\right)$.

Sketch the curve $y=f\left(x\right)$, 0 ≤ $x$ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.

Write down the gradient of the curve of $f$ at P.

Find the equation of the normal to the curve of $f$ at P.

Determine the concavity of the graph of $f$ when and justify your answer.

Find the value of $p$.

Write down the coordinates of A.

Write down the rate of change of $f$ at A.

Find the coordinates of B.

Find the the rate of change of $f$ at B.

Let $R$ be the region enclosed by the graph of $f$ , the $x$-axis, the line $x=b$ and the line $x=a$. The region $R$ is rotated 360° about the $x$-axis. Find the volume of the solid formed.

Consider $f(x)=\log k(6x-3x^2)$, for , where $k>0$.

The equation $f(x)=2$ has exactly one solution. Find the value of $k$.

Find the $x$-intercepts of the graph of $f$.

Show that the area of PQRS is $18b-2b^3$.

Hence find the value of $b$ such that the area of PQRS is a maximum.

Show that when the graphs of $f$ and $g$ intersect, $2x^2-6x+k=0$.

Given that the graphs of $f$ and $g$ intersect only once, find the value of $k$.

Express h in terms of r.

Show that $C=20\pi r^2+\frac{320\pi }{r}$.

Given that there is a minimum value for C, find this minimum value in terms of $\pi$.

Find the coordinates of P.

Find $f^{\prime }\left(x\right)$.

Hence, find the equation of L in terms of $a$.

The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$.

Find the volume of the container.

Find the value of $p$ and of $q$.

During the interval $p$ < $t$ < $q$, he volume of water in the container increases by $k$ m³. Find the value of $k$.

When $t$ = 0, the volume of water in the container is 2.3 m³. It is known that the container is never completely full of water during the 4 hour period.

Find the minimum volume of empty space in the container during the 4 hour period.

(i)     Find the value of $c$.

(ii)     Show that $b=\frac{\pi }{6}$.

(iii)     Find the value of $a$.

(i)     Write down the value of $k$.

(ii)     Find $g(x)$.

(i)     Find $w$.

(ii)     Hence or otherwise, find the maximum positive rate of change of $g$.

Sketch the graph of $f^{″}$ on the grid below:

Find the $x$-coordinates of the points of inflexion of the graph of $f$.

Hence find the values of $x$ for which the graph of $f$ is concave-down.

Find the population of fish at $t$ = 10.

Find the rate at which the population of fish is increasing at $t$ = 10.

Find the value of $t$ for which the population of fish is increasing most rapidly.

Find the cost of producing 70 shirts.

Find the value of s.

Find the number of shirts produced when the cost of production is lowest.

Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of cheese is 8 EUR.

Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of cheese is 8 EUR.

Write down an expression for $W$ in terms of $p$.

Find the price, $p$, that will give Maria the highest weekly profit.

Write down a formula for $A$, the surface area to be coated.

Express this volume in $\text{c}{\text{m}}^3$.

Write down, in terms of $r$ and $h$, an equation for the volume of this water container.

Show that $A=\pi r^2+\frac{1000000}{r}$.

Find $\frac{\text{d}A}{\text{d}r}$.

Using your answer to part (e), find the value of $r$ which minimizes $A$.

Find the value of this minimum area.

Find the least number of cans of water-resistant material that will coat the area in part (g).

Calculate the area of cloth, in cm², needed to make Haruka’s bag.

Calculate the volume, in cm³, of the bag.

Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.

Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.

Use your answers to parts (c) and (d) to show that

$A=3x^2+\frac{10368}{x}$.

Find $\frac{\text{d}A}{\text{d}x}$.

Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.

The cloth used to make Nanako’s bag costs 4 Japanese Yen (JPY) per cm².

Find the cost of the cloth used to make Nanako’s bag.

Write down an equation for the area, $A$, of the curved surface in terms of $r$.

Find $\frac{\text{d}A}{\text{d}r}$.

Find the value of $r$ when the area of the curved surface is maximized.

Find the value of $P$ if no vases are sold.

Differentiate $P\left(x\right)$.

Write down an expression for $V$, the volume (cm³) of the speaker, in terms of $r$, $l$ and $\mathrm{\pi }$.

Write down an equation for the surface area of the speaker in terms of $r$, $l$ and $\mathrm{\pi }$.

Given the design constraint that $l=\frac{150-2\mathrm{\pi }{r}^2}{\mathrm{\pi }r}$, show that $V=150r-\frac{2\mathrm{\pi }{r}^3}{3}$.

Find $\frac{\text{d}V}{\text{d}r}$.

Using your answer to part (d), show that $V$ is a maximum when $r$ is equal to $\sqrt{\frac{75}{\mathrm{\pi }}} \text{cm}$.

Find the length of the cylinder for which $V$ is a maximum.

Calculate the maximum value of $V$.

Use your answer to part (f) to identify the shape of the speaker with the best quality of sound.

Let $f(x)=15-x^2$, for $x\in \mathbb{R}$. The following diagram shows part of the graph of $f$ and the rectangle OABC, where A is on the negative $x$-axis, B is on the graph of $f$, and C is on the $y$-axis.

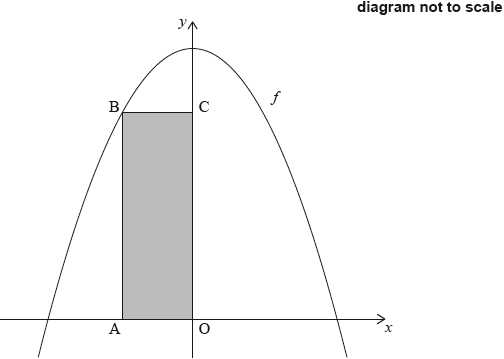
Find the $x$-coordinate of A that gives the maximum area of OABC.