IB Questionbank

User interface language: English | Español

Date	May 2019	Marks available	2	Reference code	19M.1.SL.TZ1.S_8
Level	Standard Level	Paper	Paper 1	Time zone	Time zone 1
Command term	Show that	Question number	S_8	Adapted from	N/A

Question

Let $f(x) = 9 - {x^2}$ , $x \in \mathbb{R}$ .

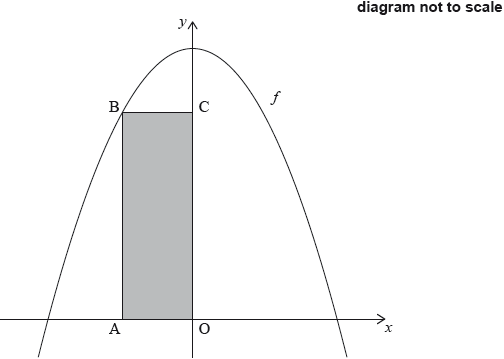
The following diagram shows part of the graph of $f$ .

Rectangle PQRS is drawn with P and Q on the $x$ -axis and R and S on the graph of $f$ .

Let OP = $b$ .

Consider another function $g(x) = {\left( {x - 3} \right)^2} + k$ , $x \in \mathbb{R}$ .

Find the $x$ -intercepts of the graph of $f$ .

[2]

Show that the area of PQRS is $18b - 2{b^3}$ .

[2]

Hence find the value of $b$ such that the area of PQRS is a maximum.

[5]

Show that when the graphs of $f$ and $g$ intersect, $2{x^2} - 6x + k = 0$ .

[2]

Given that the graphs of $f$ and $g$ intersect only once, find the value of $k$ .

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid approach (M1)

eg $f(x) = 0$ , $9 - {x^2} = 0$ , one correct solution

$x = - 3$ , 3 (accept (3, 0), (−3, 0)) A1 N2

[2 marks]

valid approach (M1)

eg height = $f(b)$ , base = 2(OP) or $2b$ , $2b\left( {9 - {x^2}} \right)$ , $2b \times f(b)$

correct working that clearly leads to given answer A1

eg $2b\left( {9 - {b^2}} \right)$

Note: Do not accept sloppy notation eg $2b \times 9 - {b^2}$ .

area = $18b - 2{b^3}$ AG N0

[2 marks]

setting derivative = 0 (seen anywhere) (M1)

eg $A' = 0$ , ${\left[ {18b - 2{b^3}} \right]^\prime } = 0$

correct derivative (must be in terms of $b$ only) (seen anywhere) A2

eg $18 - 6{b^2}$ , $2b\left( { - 2b} \right) + \left( {9 - {b^2}} \right) \times 2$

correct working (A1)

eg $6{b^2} = 18$ , $b = \pm \sqrt 3$

$b = \sqrt 3$ A1 N3

[5 marks]

valid approach (M1)

eg $f = g$ , $9 - {x^2} = {\left( {x - 3} \right)^2} + k$

correct working (A1)

eg $9 - {x^2} = {x^2} - 6x + 9 + k$ , $9 - {x^2} - {x^2} + 6x - 9 - k = 0$

$2{x^2} - 6x + k = 0$ AG N0

[2 marks]

METHOD 1 (discriminant)

recognizing to use discriminant (seen anywhere) (M1)

eg Δ, ${b^2} - 4ac$

discriminant = 0 (seen anywhere) M1

correct substitution into discriminant (do not accept only in quadratic formula) (A1)

eg ${\left( { - 6} \right)^2} - 4\left( 2 \right)\left( k \right)$ , ${\left( 6 \right)^2} - 4\left( 2 \right)\left( k \right)$

correct working (A1)

eg $36 - 8k = 0$ , $8k = 36$

$k = \frac{{36}}{8}\,\,\,\,\left( { = \frac{9}{2}{\text{,}}\,\,4.5} \right)$ A1 N2

METHOD 2 (completing the square)

valid approach to complete the square (M1)

eg $2\left( {{x^2} - 3x + \frac{9}{4}} \right) = - k + \frac{{18}}{4}$ , ${x^2} - 3x + \frac{9}{4} - \frac{9}{4} + \frac{k}{2} = 0$

correct working (A1)

eg $2{\left( {x - \frac{3}{2}} \right)^2} = - k + \frac{{18}}{4}$ , ${\left( {x - \frac{3}{2}} \right)^2} - \frac{9}{4} + \frac{k}{2} = 0$

recognizing condition for one solution M1

eg ${\left( {x - \frac{3}{2}} \right)^2} = 0$ , $- \frac{9}{4} + \frac{k}{2} = 0$

correct working (A1)

eg $- k = \frac{{18}}{4}$ , $\frac{k}{2} = \frac{9}{4}$

$k = \frac{{18}}{4}\,\,\,\,\left( { = \frac{9}{2}{\text{,}}\,\,4.5} \right)$ A1 N2

METHOD 3 (using vertex)

valid approach to find vertex (seen anywhere) M1

eg ${\left( {2{x^2} - 6x + k} \right)^\prime } = 0$ , $- \frac{b}{{2a}}$

correct working (A1)

eg ${\left( {2{x^2} - 6x + k} \right)^\prime } = 4x - 6$ , $- \frac{{\left( { - 6} \right)}}{{2\left( 2 \right)}}$

$x = \frac{6}{4}\,\,\left( { = \frac{3}{2}} \right)$ (A1)

correct substitution (A1)

eg $2{\left( {\frac{3}{2}} \right)^2} - 6\left( {\frac{3}{2}} \right) + k = 0$

$k = \frac{{18}}{4}\,\,\,\,\left( { = \frac{9}{2}{\text{,}}\,\,4.5} \right)$ A1 N2

[5 marks]

Examiners report

[N/A]

Syllabus sections

Topic 5—Calculus » SL 5.7—Optimisation

Show 119 related questions

18M.1.AHL.TZ1.H_9c:
Sketch the graph of $y = f\left( x \right)$ showing clearly the position of the points A and B.
22M.2.SL.TZ2.5c.ii:
Use the model to find how much coffee the cafe should make each morning to maximize its profit.
17M.1.AHL.TZ2.H_10a.i:
Find the area of the window in terms of P and $r$ .
18M.1.SL.TZ2.T_13b:
Find the value of s.
18N.2.SL.TZ0.T_6a:
Calculate the area of cloth, in cm², needed to make Haruka’s bag.
18N.2.SL.TZ0.T_6e:
Use your answers to parts (c) and (d) to show that

$A = 3{x^2} + \frac{{10368}}{x}$ .
22M.2.SL.TZ1.4c:
Find the value of $t$ at which the goat is eating grass at the greatest rate.
22M.2.AHL.TZ1.2c:
Find the value of $t$ at which the goat is eating grass at the greatest rate.
21N.1.SL.TZ0.12b.i:
Solve $S' (x) = 0$ .
21N.1.AHL.TZ0.15b.i:
Find an expression for $V$ in terms of $θ$ .
21N.1.AHL.TZ0.15b.ii:
Find the expression $\frac{d V}{d θ}$ .
21N.1.AHL.TZ0.15b.iii:
Solve algebraically $\frac{d V}{d θ} = 0$ to find the value of $θ$ that will maximize the volume, $V$ .
16N.2.SL.TZ0.T_6b:
Express this volume in ${\text{c}}{{\text{m}}^3}$ .
SPM.2.SL.TZ0.4d:
Find $P\left( x \right)$ .
17M.1.SL.TZ1.S_6a.i:
Write down the gradient of the curve of $f$ at P.
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
19M.2.SL.TZ1.S_4a:
Sketch the graph of ${f''}$ on the grid below:
19M.2.SL.TZ2.S_5a:
Find the population of fish at $t$ = 10.
18M.1.SL.TZ2.T_13c:
Find the number of shirts produced when the cost of production is lowest.
18N.2.SL.TZ0.T_6b:
Calculate the volume, in cm³, of the bag.
17M.1.AHL.TZ2.H_10a.ii:
Find the width of the window in terms of P when the area is a maximum, justifying that this is a maximum.
17M.1.AHL.TZ2.H_10b:
Show that in this case the height of the rectangle is equal to the radius of the semicircle.
18M.1.SL.TZ2.S_9c:
Given that there is a minimum value for C, find this minimum value in terms of $\pi$ .
18M.1.SL.TZ2.T_13a:
Find the cost of producing 70 shirts.
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of $f$ at A.
18N.2.SL.TZ0.T_6h:
The cloth used to make Nanako’s bag costs 4 Japanese Yen (JPY) per cm².

Find the cost of the cloth used to make Nanako’s bag.
19M.1.AHL.TZ1.H_8d:
Sketch the curve $y = f\left( x \right)$ , 0 ≤ $x$ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.
SPM.2.SL.TZ0.4a:
Calculate the surface area of the box in cm².
19N.2.SL.TZ0.T_6c:
Given the design constraint that $l = \frac{150 - 2 π r^{2}}{π r}$ , show that $V = 150 r - \frac{2 π r^{3}}{3}$ .
19M.2.SL.TZ1.S_4b:
Find the $x$ -coordinates of the points of inflexion of the graph of $f$ .
19M.1.SL.TZ1.T_15c:
Find the value of $r$ when the area of the curved surface is maximized.
19M.2.SL.TZ2.S_5b:
Find the rate at which the population of fish is increasing at $t$ = 10.
19N.2.SL.TZ0.T_6e:
Using your answer to part (d), show that $V$ is a maximum when $r$ is equal to $\sqrt{\frac{75}{π}} cm$ .
19N.2.SL.TZ0.T_6h:
Use your answer to part (f) to identify the shape of the speaker with the best quality of sound.
18N.2.SL.TZ0.T_6f:
Find $\frac{{{\text{d}}A}}{{{\text{d}}x}}$ .
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
19M.1.SL.TZ1.S_8e:
Given that the graphs of $f$ and $g$ intersect only once, find the value of $k$ .
17N.1.SL.TZ0.T_15b:
Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of cheese is 8 EUR.
19M.2.SL.TZ1.S_4c:
Hence find the values of $x$ for which the graph of $f$ is concave-down.
19N.2.SL.TZ0.T_6g:
Calculate the maximum value of $V$ .
18N.1.SL.TZ0.S_10b.ii:
Hence, find the equation of L in terms of $a$ .
18N.1.SL.TZ0.S_10a:
Find the coordinates of P.
17N.1.SL.TZ0.S_7:
Consider $f(x) = \log k(6x - 3{x^2})$ , for $0 < x < 2$ , where $k > 0$ .

The equation $f(x) = 2$ has exactly one solution. Find the value of $k$ .
16N.2.SL.TZ0.S_10a:
(i) Find the value of $c$ .

(ii) Show that $b = \frac{\pi }{6}$ .

(iii) Find the value of $a$ .
18N.2.SL.TZ0.T_6d:
Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.
17M.1.SL.TZ1.S_6b:
Determine the concavity of the graph of $f$ when $4 < x < 5$ and justify your answer.
19M.1.SL.TZ2.T_15a:
Find the value of $P$ if no vases are sold.
19N.2.SL.TZ0.T_6f:
Find the length of the cylinder for which $V$ is a maximum.
19M.1.AHL.TZ2.H_8b:
Given that there is one inscribed cone having a maximum volume, show that the volume of this cone is $\frac{{32\pi {R^3}}}{{81}}$ .
18N.2.SL.TZ0.T_6g:
Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.
19N.2.SL.TZ0.T_6d:
Find $\frac{d V}{d r}$ .
18N.1.SL.TZ0.S_10b.i:
Find $f'\left( x \right)$ .
17M.1.SL.TZ1.S_6a.ii:
Find the equation of the normal to the curve of $f$ at P.
18N.1.SL.TZ0.S_10c:
The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$ .
19N.2.SL.TZ0.T_6a:
Write down an expression for $V$ , the volume (cm³) of the speaker, in terms of $r$ , $l$ and $π$ .
19M.1.AHL.TZ1.H_8a:
Write down the $x$ -coordinate of the point of inflexion on the graph of $y = f\left( x \right)$ .
19M.1.SL.TZ2.T_15b:
Differentiate $P\left( x \right)$ .
18M.1.AHL.TZ1.H_9b.i:
Show that there is exactly one point of inflexion, B, on the graph of $y = f\left( x \right)$ .
18M.1.AHL.TZ1.H_9a:
The graph of $y = f\left( x \right)$ has a local maximum at A. Find the coordinates of A.
18N.2.SL.TZ0.S_10c:
When $t$ = 0, the volume of water in the container is 2.3 m³. It is known that the container is never completely full of water during the 4 hour period.

Find the minimum volume of empty space in the container during the 4 hour period.
18M.1.AHL.TZ2.H_4:
Consider the curve $y = \frac{1}{{1 - x}} + \frac{4}{{x - 4}}$ .

Find the x-coordinates of the points on the curve where the gradient is zero.
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of $r$ which minimizes $A$ .
18N.2.SL.TZ0.T_6c:
Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.
18M.2.AHL.TZ1.H_9a:
Show that there are exactly two points on the curve where the gradient is zero.
20N.2.SL.TZ0.T_4a:
Write down an equation in $r$ and $h$ that shows this information.
20N.2.SL.TZ0.T_4d:
Using your answer to part (c), find the value of $h$ for which $V$ is a maximum.
19M.1.SL.TZ1.S_8b:
Show that the area of PQRS is $18b - 2{b^3}$ .
16N.2.SL.TZ0.S_10b:
(i) Write down the value of $k$ .

(ii) Find $g(x)$ .
17M.2.SL.TZ2.S_8d:
Let $R$ be the region enclosed by the graph of $f$ , the $x$ -axis, the line $x = b$ and the line $x = a$ . The region $R$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
16N.2.SL.TZ0.T_6e:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
17M.2.SL.TZ2.S_8a:
Find the value of $p$ .
18M.1.SL.TZ2.S_9b:
Show that $C = 20\pi {r^2} + \frac{{320\pi }}{r}$ .
19M.2.SL.TZ2.S_5c:
Find the value of $t$ for which the population of fish is increasing most rapidly.
18N.2.SL.TZ0.S_10a:
Find the volume of the container.
17N.1.SL.TZ0.S_6:
Let $f(x) = 15 - {x^2}$ , for $x \in \mathbb{R}$ . The following diagram shows part of the graph of $f$ and the rectangle OABC, where A is on the negative $x$ -axis, B is on the graph of $f$ , and C is on the $y$ -axis.

Find the $x$ -coordinate of A that gives the maximum area of OABC.
SPM.2.SL.TZ0.4e:
Find the least number of boxes which must be sold each week in order to make a profit.
18M.1.AHL.TZ1.H_9b.ii:
The coordinates of B can be expressed in the form B $\left( {{2^a},\,b \times {2^{ - 3a}}} \right)$ where a, b $\in \mathbb{Q}$ . Find the value of a and the value of b.
17N.1.SL.TZ0.T_15a:
Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of cheese is 8 EUR.
18M.2.AHL.TZ1.H_9d:
The shaded region is rotated by 2 $\pi$ about the $y$ -axis. Find the volume of the solid formed.
18N.2.SL.TZ0.S_10b.ii:
During the interval $p$ < $t$ < $q$ , he volume of water in the container increases by $k$ m³. Find the value of $k$ .
20N.2.SL.TZ0.T_4e:
Find the maximum volume of the bird bath.
17N.1.SL.TZ0.T_15d:
Find the price, $p$ , that will give Maria the highest weekly profit.
SPM.2.SL.TZ0.4b:
Calculate the length AG.
17N.1.SL.TZ0.T_15c:
Write down an expression for $W$ in terms of $p$ .
19M.1.AHL.TZ1.H_8b:
find the value of $f\left( 1 \right)$ .
20N.2.SL.TZ0.T_4c:
Find $\frac{d V}{d h}$ .
21M.1.SL.TZ2.13a:
Find an expression for $P$ in terms of $x$ .
20N.2.SL.TZ0.T_4b:
Show that $V = \frac{2500 π h}{3} - \frac{π h^{3}}{3}$ .
16N.2.SL.TZ0.T_6c:
Write down, in terms of $r$ and $h$ , an equation for the volume of this water container.
16N.2.SL.TZ0.T_6a:
Write down a formula for $A$ , the surface area to be coated.
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
21M.2.SL.TZ1.5a.ii:
Hence find the maximum height of the tunnel.
21M.2.AHL.TZ1.2a.ii:
Hence find the maximum height of the tunnel.
18N.2.SL.TZ0.S_10b.i:
Find the value of $p$ and of $q$ .
16N.2.SL.TZ0.T_6d:
Show that $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ .
SPM.2.SL.TZ0.4c:
Find the number of boxes that should be sold each week to maximize the profit.
16N.2.SL.TZ0.S_10c:
(i) Find $w$ .

(ii) Hence or otherwise, find the maximum positive rate of change of $g$ .
18M.2.AHL.TZ1.H_9c:
The normal at P cuts the curve again at the point Q. Find the $x$ -coordinate of Q.
19M.1.SL.TZ1.S_8a:
Find the $x$ -intercepts of the graph of $f$ .
19N.2.SL.TZ0.T_6b:
Write down an equation for the surface area of the speaker in terms of $r$ , $l$ and $π$ .
19M.1.SL.TZ1.S_8c:
Hence find the value of $b$ such that the area of PQRS is a maximum.
21M.1.SL.TZ2.13b:
The company regularly increases the number of cars it produces.

Describe how their profit changes if they increase production to over $30$ cars per month and up to $50$ cars per month. Justify your answer.
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, $A$ , of the curved surface in terms of $r$ .
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
18M.2.AHL.TZ1.H_9b:
Find the equation of the normal to the curve at the point P.
19M.1.AHL.TZ1.H_8c:
find the value of $f\left( 4 \right)$ .
18M.1.SL.TZ2.S_9a:
Express h in terms of r.
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of $f$ at B.
19M.1.SL.TZ1.T_15b:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
19M.1.AHL.TZ2.H_8a:
Show that the volume of the cone may be expressed by $V = \frac{\pi }{3}\left( {2R{h^2} - {h^3}} \right)$ .
20N.2.SL.TZ0.T_4f:
To prevent leaks, a sealant is applied to the interior surface of the bird bath.

Find the surface area to be covered by the sealant, given that the bird bath has maximum volume.
EXN.2.SL.TZ0.2e:
Hence or otherwise find the minimum length of ribbon required.
21N.1.AHL.TZ0.15a:
Show that $r = \frac{6}{2 + θ}$ .
EXN.2.SL.TZ0.2a:
Find an expression for the total length of the ribbon $L$ in terms of $x$ and $y$ .
EXN.2.SL.TZ0.2b:
Show that $L = 2 x + \frac{300}{x} + 22$
EXN.2.SL.TZ0.2c:
Find $\frac{d L}{d x}$
EXN.2.SL.TZ0.2d:
Solve $\frac{d L}{d x} = 0$
21N.1.SL.TZ0.12a:
Find $S' (x)$ .
21N.1.SL.TZ0.12b.ii:
Interpret your answer to (b)(i) in context.

Hide related questions

Topic 5—Calculus

Question

Markscheme

Examiners report

Syllabus sections

View options