| Date | May 2022 | Marks available | 2 | Reference code | 22M.1.SL.TZ2.2 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 2 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
A group of applicants applied for admission into either the Arts programme or the Sciences programme at a university. The outcomes of their applications are shown in the following table.
An applicant is chosen at random from this group. It is found that they were accepted into the programme of their choice.
Find the probability that a randomly chosen applicant from this group was accepted by the university.
Find the probability that the applicant applied for the Arts programme.
Two different applicants are chosen at random from the original group.
Find the probability that both applicants applied to the Arts programme.
Markscheme
A1
[1 mark]
A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
Award A1A0 for working of if followed by an incorrect answer.
[2 marks]
A1M1
Note: Award A1 for two correct fractions seen, M1 for multiplying their fractions.
A1
[3 marks]
Examiners report
Candidates are reasonably proficient at calculating simple probabilities from a table.
Several candidates did not consider the condition, with some merely finding the probability of an applicant applying for Arts programme with no condition, some considering those who were accepted into Arts with no condition, and some finding the probability of being accepted into Arts given the condition that they applied for Arts.
Only a few candidates recognized dependent events, with most calculating as if the events were independent.
Syllabus sections
-
19M.1.SL.TZ1.T_7b:
In the table indicate which two of the given statements are true by placing a tick (✔) in the right hand column.
-
18M.2.SL.TZ2.T_1a.i:
Write down the value of a.
-
22M.1.SL.TZ2.5a:
Calculate the expected number of people who will pass this polygraph test.
-
22M.1.SL.TZ2.5c:
Determine the probability that fewer than people will pass this polygraph test.
-
18N.2.SL.TZ0.T_2a.i:
Find the number of students in the school that are taught in Spanish.
-
18M.1.SL.TZ2.S_8a:
Copy and complete the following tree diagram.
-
18M.1.SL.TZ1.T_10a:
Complete the Venn diagram using the given information.
-
17M.1.SL.TZ2.T_2b:
Complete the Venn diagram using the above information.
-
18M.1.SL.TZ2.T_9a.i:
Write down an expression, in set notation, for the shaded region represented by Diagram 1.
-
19M.1.SL.TZ1.T_7a:
Place the numbers and in the correct position on the Venn diagram.
-
18M.1.SL.TZ2.T_9b.i:
Shade, on the Venn diagram, the region represented by the set .
-
19M.1.SL.TZ2.T_11b.ii:
Write down .
-
17M.1.SL.TZ1.S_1b:
A girl is selected at random. Find the probability that she takes economics but not history.
-
18M.2.SL.TZ2.T_1a.ii:
Write down the value of b.
-
22M.2.SL.TZ1.5c:
Find, to the nearest integer, the expected increase or decrease in the money made by the airline if they decide to sell tickets rather than .
-
21N.1.SL.TZ0.11a:
Write down the value of .
-
21N.1.SL.TZ0.11b:
Find an expression, in terms of , for the probability of a person not having blue eyes and having fair hair.
-
21N.2.SL.TZ0.3f.ii:
The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.
At any given instant, find the probability that Tim can see point from his window. Justify your answer.
-
21N.2.SL.TZ0.3e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
22M.1.SL.TZ2.5b:
Calculate the probability that exactly people will fail this polygraph test.
-
22M.1.SL.TZ2.2c:
Two different applicants are chosen at random from the original group.
Find the probability that both applicants applied to the Arts programme.
-
22M.1.SL.TZ2.2a:
Find the probability that a randomly chosen applicant from this group was accepted by the university.
-
21N.1.SL.TZ0.11c.i:
.
-
21N.1.SL.TZ0.11c.ii:
.
-
21N.2.SL.TZ0.1b:
State the null and alternative hypotheses.
-
21N.2.SL.TZ0.3c.i:
Write down the amplitude of the function.
-
21N.2.SL.TZ0.3e.i:
Find the height of above the ground when .
-
19M.2.AHL.TZ2.H_3a:
Complete the given probability tree diagram for Iqbal’s three attempts, labelling each branch with the correct probability.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
17M.1.SL.TZ1.T_4b:
Determine whether rock-climbing is offered by the school in the fall/autumn trimester.
-
16N.2.SL.TZ0.T_2c:
Write down the value of .
-
18N.2.SL.TZ0.T_2a.ii:
Find the number of students in the school that study Mathematics in English.
-
17M.2.SL.TZ2.S_10b.i:
Write down the probability of drawing three blue marbles.
-
18M.2.SL.TZ2.T_1c.i:
Find the value of x.
-
18M.2.SL.TZ2.T_1c.ii:
Find the value of y.
-
17M.1.SL.TZ2.T_2d:
Write down the value of .
-
17M.1.SL.TZ1.S_1a.i:
Find the value of ;
-
19M.1.SL.TZ2.T_11a:
Write down the elements that belong to .
-
18M.2.SL.TZ2.T_1d:
Find the number of employees who, in the last year, did not travel to work by car, bicycle or public transportation.
-
19N.2.SL.TZ0.T_1d.ii:
the -value.
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
18M.1.SL.TZ2.T_9b.ii:
Shade, on the Venn diagram, the region represented by the set .
-
18M.1.SL.TZ2.S_8d:
Given that Pablo is late for work, find the probability that he left home before 07:00.
-
19M.1.SL.TZ1.S_1b:
Find the value of .
-
19M.1.SL.TZ1.S_1c:
Find .
-
17M.1.SL.TZ1.T_4a:
Write down the number of sporting activities offered by the school during its school year.
-
18M.2.SL.TZ2.T_1e:
Find .
-
18M.1.SL.TZ2.S_8b:
Find the probability that Pablo leaves home before 07:00 and is late for work.
-
18N.1.SL.TZ0.S_9c:
Hayley plays the game when = 5. She pays $20 to play and can earn money back depending on the number of draws it takes to obtain a blue marble. She earns no money back if she obtains a blue marble on her first draw. Let M be the amount of money that she earns back playing the game. This information is shown in the following table.
Find the value of so that this is a fair game.
-
18N.2.SL.TZ0.T_2c.i:
Find the probability that this student studies Mathematics.
-
17N.1.SL.TZ0.S_1b:
Find the probability that exactly one of the selected balls is green.
-
16N.1.SL.TZ0.T_3a:
In the table indicate whether the given statements are True or False.
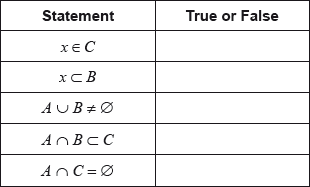
-
19N.2.SL.TZ0.T_1d.i:
the statistic.
-
19N.2.SL.TZ0.T_1b:
Write down the number of degrees of freedom.
-
19N.2.SL.TZ0.T_1a:
State , the null hypothesis for this test.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
18N.2.SL.TZ0.T_2a.iii:
Find the number of students in the school that study both Biology and Mathematics.
-
18M.1.SL.TZ2.S_8c:
Find the probability that Pablo is late for work.
-
17N.1.SL.TZ0.S_1a:
Complete the following tree diagram.
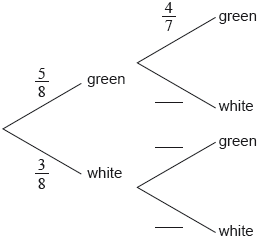
-
17M.1.SL.TZ1.T_4c.i:
Write down the elements of the set ;
-
19N.2.SL.TZ0.T_1f.ii:
Calculate the probability that the customer is an adult or that the customer chose shrimp.
-
18M.1.SL.TZ1.T_10c:
Write down the value of .
-
19N.2.SL.TZ0.T_1f.iii:
Given that the customer is a child, calculate the probability that they chose pasta or fish.
-
18M.2.SL.TZ1.S_5a:
Find P(A ∩ B′ ).
-
18M.1.SL.TZ2.T_9a.ii:
Write down an expression, in set notation, for the shaded region represented by Diagram 2.
-
18N.2.SL.TZ0.T_2b.ii:
Write down .
-
17M.1.SL.TZ1.T_4c.ii:
Write down .
-
16N.1.SL.TZ0.T_3b:
On the Venn diagram, shade the region .
-
17M.2.AHL.TZ2.H_5a:
Draw a tree diagram to represent this information for the first three days of July.
-
18N.1.SL.TZ0.S_9a.i:
Find the probability, in terms of , that the game will end on her first draw.
-
19N.2.SL.TZ0.T_1e:
State the conclusion for this test. Give a reason for your answer.
-
19N.2.SL.TZ0.T_1c:
Show that the expected number of children who chose shrimp is , correct to two significant figures.
-
17M.2.AHL.TZ2.H_5c:
Find the probability that the 1st July was calm given that the 3rd July is windy.
-
17M.1.SL.TZ2.T_2c:
Find the number of children who play only football.
-
17M.2.AHL.TZ2.H_1a:
One of the players is chosen at random. Find the probability that this player’s score was 5 or more.
-
18M.2.SL.TZ2.T_1b.ii:
Use the tree diagram to find the probability that an employee was late for work.
-
18N.1.SL.TZ0.S_9b.ii:
fourth draw.
-
19M.2.AHL.TZ2.H_3c:
Find the probability that Iqbal passes his third paper, given that he passed only one previous paper.
-
18M.1.SL.TZ2.S_8e:
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
-
17N.1.SL.TZ0.T_7b:
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
-
16N.2.SL.TZ0.T_2b:
Show that .
-
18M.2.SL.TZ2.T_1b.i:
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
SPM.1.SL.TZ0.13a:
Find the probability that on any given day Mr Burke chooses a female student to answer a question.
-
18N.2.SL.TZ0.T_2b.i:
Write down .
-
19N.2.SL.TZ0.T_1f.i:
Calculate the probability that the customer is an adult.
-
20N.1.SL.TZ0.S_8a:
Find the value of .
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.1.SL.TZ0.T_6a.ii:
Find the probability that the first ball chosen is labelled or labelled .
-
17M.2.SL.TZ2.S_10d:
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
-
20N.1.SL.TZ0.S_8b:
Write down the value of the median distance in kilometres (km).
-
20N.1.SL.TZ0.S_8d:
Find .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
16N.2.SL.TZ0.T_6e:
Find .
-
19N.1.SL.TZ0.T_9b:
Find the probability that Sungwon scores greater than on both of her first two turns.
-
17N.1.SL.TZ0.T_7c:
Determine whether the events and are independent.
-
17M.2.AHL.TZ2.H_5b:
Find the probability that the 3rd July is calm.
-
16N.1.SL.TZ0.S_5a:
Find .
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
17M.1.SL.TZ2.T_2a:
Write down an expression, in terms of , for the number of children who play only basketball.
-
18M.1.SL.TZ2.T_9a.iii:
Write down an expression, in set notation, for the shaded region represented by Diagram 3.
-
SPM.1.SL.TZ0.13b:
Find the probability he will choose a female student 8 times.
-
18M.1.SL.TZ1.T_10b:
Find the value of x.
-
17M.2.SL.TZ2.S_10a.i:
Find .
-
18M.2.SL.TZ1.S_5b:
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
-
SPM.1.SL.TZ0.13c:
Find the probability he will choose a male student at most 9 times.
-
17N.1.SL.TZ0.T_7a:
Complete the Venn diagram for these students.
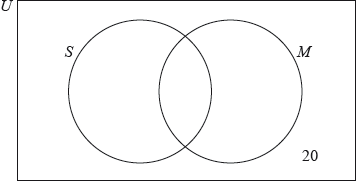
-
17M.1.SL.TZ1.S_1a.ii:
Find the value of .
-
19N.1.SL.TZ0.T_9a:
Find the probability that Sungwon’s score on her first turn is greater than .
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.1.SL.TZ0.S_8c:
Find the value of .
-
19M.2.AHL.TZ2.H_3b:
Calculate the probability that Iqbal passes at least two of the papers he attempts.
-
20N.1.SL.TZ0.T_6c:
Find the probability that both balls chosen are labelled .
-
20N.1.SL.TZ0.T_6a.i:
Find the probability that the first ball chosen is labelled .
-
20N.1.SL.TZ0.S_8e:
The first athletes that completed the race won a prize.
Given that an athlete took between and minutes to complete the race, calculate the probability that they won a prize.
-
17M.2.SL.TZ2.S_B10c:
Jill plays the game nine times. Find the probability that she wins exactly two prizes.
-
18N.1.SL.TZ0.S_9b.i:
third draw.
-
17M.2.SL.TZ2.S_10b.ii:
Explain why the probability of drawing three white marbles is .
-
16N.2.SL.TZ0.T_2a:
Draw a Venn diagram to represent the given information, using sets labelled , and .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
17M.2.SL.TZ2.S_10a.ii:
Find .
-
17M.1.SL.TZ1.T_4d:
Write down, in terms of , and , an expression for the set which contains only archery, baseball, kayaking and surfing.
-
19M.1.SL.TZ1.S_1a:
Find the value of .
-
16N.2.SL.TZ0.T_6d:
Show that .
-
19N.1.SL.TZ0.T_9c:
Sungwon will play the game for turns.
Find the expected number of times the score on a turn is greater than .
-
17M.2.AHL.TZ2.H_1b:
Calculate the mean score.
-
18N.2.SL.TZ0.T_2c.ii:
Find the probability that this student studies neither Biology nor Mathematics.
-
20N.1.SL.TZ0.T_6b:
Find the probability that the second ball chosen is labelled , given that the first ball chosen was labelled .
-
17M.2.SL.TZ2.S_10b.iii:
The bag contains a total of ten marbles of which are white. Find .
-
19M.1.SL.TZ2.T_11b.i:
Write down the elements that belong to .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.1.SL.TZ0.S_5b:
Find .
-
18N.1.SL.TZ0.S_9a.ii:
Find the probability, in terms of , that the game will end on her second draw.
-
18M.2.SL.TZ2.T_1b.iii:
Use the tree diagram to find the probability that an employee encountered traffic given that they were late for work.
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
18N.2.SL.TZ0.T_2c.iii:
Find the probability that this student is taught in Spanish, given that the student studies Biology.
-
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
16N.2.SL.TZ0.T_2d:
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
-
21N.2.SL.TZ0.1a.i:
prefers a tablet.
-
21N.2.SL.TZ0.1a.ii:
is years old and prefers a mobile phone.
-
21N.2.SL.TZ0.1a.iii:
prefers a laptop given that they are years old.
-
21N.2.SL.TZ0.1a.iv:
prefers a tablet or is years old.
-
21N.2.SL.TZ0.1c:
Write down the number of degrees of freedom.
-
21N.2.SL.TZ0.1d.i:
Write down the test statistic.
-
21N.2.SL.TZ0.1d.ii:
Write down the -value.
-
21N.2.SL.TZ0.1d.iii:
State the conclusion for the test in context. Give a reason for your answer.
-
21N.2.SL.TZ0.3a.i:
maximum value of .
-
21N.2.SL.TZ0.3a.ii:
minimum value of .
-
21N.2.SL.TZ0.3b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.SL.TZ0.3b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.SL.TZ0.3c.ii:
Find the period of the function.
-
21N.2.SL.TZ0.3d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.SL.TZ0.3f.i:
At any given instant, find the probability that point is visible from Tim’s window.

