| Date | November 2021 | Marks available | 1 | Reference code | 21N.1.SL.TZ0.11 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Write down | Question number | 11 | Adapted from | N/A |
Question
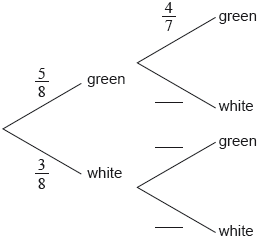
In a city, of people have blue eyes. If someone has blue eyes, the probability that they also have fair hair is . This information is represented in the following tree diagram.
It is known that of people in this city have fair hair.
Calculate the value of
Write down the value of .
Find an expression, in terms of , for the probability of a person not having blue eyes and having fair hair.
.
.
Markscheme
A1
[1 mark]
A1
[1 mark]
(M1)
Note: Award (M1) for setting up equation for fair-haired or equivalent.
A1
[2 marks]
A1
[1 mark]
Examiners report
Despite its position on the paper, this probability question was reasonably well attempted by most candidates. Many candidates were able to score at least the first mark and the final FT mark. Even the weaker candidates recognized that probabilities added to in part (c)(ii). Parts (b) and (c)(i) seemed to be the most difficult part for the less able candidates.
Despite its position on the paper, this probability question was reasonably well attempted by most candidates. Many candidates were able to score at least the first mark and the final FT mark. Even the weaker candidates recognized that probabilities added to in part (c)(ii). Parts (b) and (c)(i) seemed to be the most difficult part for the less able candidates.
Despite its position on the paper, this probability question was reasonably well attempted by most candidates. Many candidates were able to score at least the first mark and the final FT mark. Even the weaker candidates recognized that probabilities added to in part (c)(ii). Parts (b) and (c)(i) seemed to be the most difficult part for the less able candidates.
Despite its position on the paper, this probability question was reasonably well attempted by most candidates. Many candidates were able to score at least the first mark and the final FT mark. Even the weaker candidates recognized that probabilities added to in part (c)(ii). Parts (b) and (c)(i) seemed to be the most difficult part for the less able candidates.