| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.SL.TZ2.S_10 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Find | Question number | S_10 | Adapted from | N/A |
Question
The following table shows a probability distribution for the random variable , where .
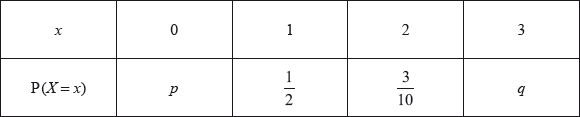
A bag contains white and blue marbles, with at least three of each colour. Three marbles are drawn from the bag, without replacement. The number of blue marbles drawn is given by the random variable .
A game is played in which three marbles are drawn from the bag of ten marbles, without replacement. A player wins a prize if three white marbles are drawn.
Find .
Find .
Write down the probability of drawing three blue marbles.
Explain why the probability of drawing three white marbles is .
The bag contains a total of ten marbles of which are white. Find .
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
Markscheme
correct substitution into formula (A1)
eg
, 0.0333 A1 N2
[2 marks]
evidence of summing probabilities to 1 (M1)
eg
A1 N2
[2 marks]
A1 N1
[1 mark]
valid reasoning R1
eg
AG N0
[1 mark]
valid method (M1)
eg
correct equation A1
eg
A1 N2
[3 marks]
recognizing one prize in first seven attempts (M1)
eg
correct working (A1)
eg
correct approach (A1)
eg
0.065119
0.0651 A1 N2
[4 marks]