| Date | May 2019 | Marks available | 3 | Reference code | 19M.2.SL.TZ1.S_10 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Find | Question number | S_10 | Adapted from | N/A |
Question
There are three fair six-sided dice. Each die has two green faces, two yellow faces and two red faces.
All three dice are rolled.
Ted plays a game using these dice. The rules are:
- Having a turn means to roll all three dice.
- He wins $10 for each green face rolled and adds this to his winnings.
- After a turn Ted can either:
- end the game (and keep his winnings), or
- have another turn (and try to increase his winnings).
- If two or more red faces are rolled in a turn, all winnings are lost and the game ends.
The random variable ($) represents how much is added to his winnings after a turn.
The following table shows the distribution for , where $ represents his winnings in the game so far.
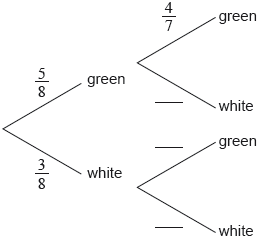
Find the probability of rolling exactly one red face.
Find the probability of rolling two or more red faces.
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
Write down the value of .
Hence, find the value of .
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
Markscheme
valid approach to find P(one red) (M1)
eg , , ,
listing all possible cases for exactly one red (may be indicated on tree diagram)
P(1 red) = 0.444 [0.444, 0.445] A1 N2
[3 marks] [5 maximum for parts (a.i) and (a.ii)]
valid approach (M1)
eg P() + P(), 1 − P( ≤ 1), binomcdf
correct working (A1)
eg , 0.222 + 0.037 ,
0.259259
P(at least two red) = 0.259 A1 N3
[3 marks] [5 maximum for parts (a.i) and (a.ii)]
recognition that winning $10 means rolling exactly one green (M1)
recognition that winning $10 also means rolling at most 1 red (M1)
eg “cannot have 2 or more reds”
correct approach A1
eg P(1G ∩ 0R) + P(1G ∩ 1R), P(1G) − P(1G ∩ 2R),
“one green and two yellows or one of each colour”
Note: Because this is a “show that” question, do not award this A1 for purely numerical expressions.
one correct probability for their approach (A1)
eg , , , ,
correct working leading to A1
eg , ,
probability = AG N0
[5 marks]
, 0.259 (check FT from (a)(ii)) A1 N1
[1 mark]
evidence of summing probabilities to 1 (M1)
eg , ,
0.148147 (0.148407 if working with their value to 3 sf)
(exact), 0.148 A1 N2
[2 marks]
correct substitution into the formula for expected value (A1)
eg
correct critical value (accept inequality) A1
eg = 34.2857 , > 34.2857
$40 A1 N2
[3 marks]