| Date | November 2016 | Marks available | 2 | Reference code | 16N.1.hl.TZ0.11 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Show that | Question number | 11 | Adapted from | N/A |
Question
Let \(y = {{\text{e}}^x}\sin x\).
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).
Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).
Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).
Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.
Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find the value of the curvature of the graph of \(f\) at the local maximum point.
Find the value \(\kappa \) for \(x = \frac{\pi }{2}\) and comment on its meaning with respect to the shape of the graph.
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x - \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
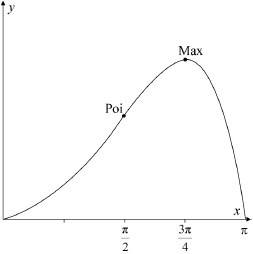
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi - \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi - \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ - {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ - {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi - \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x - [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = - \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { - \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]

