| Date | November 2015 | Marks available | 3 | Reference code | 15N.2.hl.TZ0.13 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 13 | Adapted from | N/A |
Question
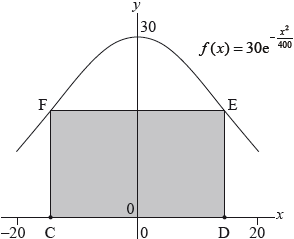
The following diagram shows a vertical cross section of a building. The cross section of the roof of the building can be modelled by the curve \(f(x) = 30{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}}\), where \( - 20 \le x \le 20\).
Ground level is represented by the \(x\)-axis.
Find \(f''(x)\).
Show that the gradient of the roof function is greatest when \(x = - \sqrt {200} \).
The cross section of the living space under the roof can be modelled by a rectangle \(CDEF\) with points \({\text{C}}( - a,{\text{ }}0)\) and \({\text{D}}(a,{\text{ }}0)\), where \(0 < a \le 20\).
Show that the maximum area \(A\) of the rectangle \(CDEF\) is \(600\sqrt 2 {{\text{e}}^{ - \frac{1}{2}}}\).
A function \(I\) is known as the Insulation Factor of \(CDEF\). The function is defined as \(I(a) = \frac{{P(a)}}{{A(a)}}\) where \({\text{P}} = {\text{Perimeter}}\) and \({\text{A}} = {\text{Area of the rectangle}}\).
(i) Find an expression for \(P\) in terms of \(a\).
(ii) Find the value of \(a\) which minimizes \(I\).
(iii) Using the value of \(a\) found in part (ii) calculate the percentage of the cross sectional area under the whole roof that is not included in the cross section of the living space.
Markscheme
\(f'(x) = 30{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}} \bullet - \frac{{2x}}{{400}}\;\;\;\left( { = - \frac{{3x}}{{20}}{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}}} \right)\) M1A1
Note: Award M1 for attempting to use the chain rule.
\(f''(x) = - \frac{3}{{20}}{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}} + \frac{{3{x^2}}}{{4000}}{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}}\;\;\;\left( { = \frac{3}{{20}}{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}}\left( {\frac{{{x^2}}}{{200}} - 1} \right)} \right)\) M1A1
Note: Award M1 for attempting to use the product rule.
[4 marks]
the roof function has maximum gradient when \(f''(x) = 0\) (M1)
Note: Award (M1) for attempting to find \(f''\left( { - \sqrt {200} } \right)\).
EITHER
\( = 0\) A1
OR
\(f''(x) = 0 \Rightarrow x = \pm \sqrt {200} \) A1
THEN
valid argument for maximum such as reference to an appropriate graph or change in the sign of \(f''(x)\) eg \(f''( - 15) = 0.010 \ldots ( > 0)\) and \(f''( - 14) = - 0.001 \ldots ( < 0)\) R1
\( \Rightarrow x = - \sqrt {200} \) AG
[3 marks]
\(A = 2a \bullet 30{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}}\;\;\;\left( { = 60a{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}} = - 400g'(a)} \right)\) (M1)(A1)
EITHER
\(\frac{{{\text{d}}A}}{{{\text{d}}a}} = 60a{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}} \bullet - \frac{a}{{200}} + 60{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}} = 0 \Rightarrow a = \sqrt {200} {\text{ }}\left( { - 400f''(a) = 0 \Rightarrow a = \sqrt {200} } \right)\) M1A1
OR
by symmetry eg \(a = - \sqrt {200} \) found in (b) or \({A_{{\text{max}}}}\) coincides with \(f''(a) = 0\) R1
\( \Rightarrow a = \sqrt {200} \) A1
Note: Award A0(M1)(A1)M0M1 for candidates who start with \(a = \sqrt {200} \) and do not provide any justification for the maximum area. Condone use of \(x\).
THEN
\({A_{{\text{max}}}} = 60 \bullet \sqrt {200} {{\text{e}}^{ - \frac{{200}}{{400}}}}\) M1
\( = 600\sqrt 2 {{\text{e}}^{ - \frac{1}{2}}}\) AG
[5 marks]
(i) perimeter \( = 4a + 60{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}}\) A1A1
Note: Condone use of \(x\).
(ii) \(I(a) = \frac{{4a + 60{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}}}}{{60a{{\text{e}}^{ - \frac{{{a^2}}}{{400}}}}}}\) (A1)
graphing \(I(a)\) or other valid method to find the minimum (M1)
\(a = 12.6\) A1
(iii) area under roof \( = \int_{ - 20}^{20} {30{{\text{e}}^{ - \frac{{{x^2}}}{{400}}}}} {\text{d}}x\) M1
\( = 896.18 \ldots \) (A1)
area of living space \( = 60 \cdot (12.6...) \cdot e - {\frac{{(12.6...)}}{{400}}^2} = 508.56...\)
percentage of empty space \( = 43.3\% \) A1
[9 marks]
Total [21 marks]

