| Date | November 2010 | Marks available | 2 | Reference code | 10N.2.SL.TZ0.B2 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | State | Question number | B2 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about a lightning discharge. Part 2 is about fuel for heating.
Part 1 Lightning discharge
The magnitude of the electric field strength \(E\) between two infinite charged parallel plates is given by the expression
\[E = \frac{\sigma }{{{\varepsilon _0}}}\]
where \(\sigma \) is the charge per unit area on one of the plates.
A thundercloud carries a charge of magnitude 35 C spread over its base. The area of the base is \(1.2 \times {10^7}{\text{ }}{{\text{m}}^{\text{2}}}\).
Part 2 Fuel for heating
A room heater burns liquid fuel and the following data are available.
\[\begin{array}{*{20}{l}} {{\text{Density of liquid fuel}}}&{ = 8.0 \times {{10}^2}{\text{ kg}}\,{{\text{m}}^{ - 3}}} \\ {{\text{Energy produced by 1 }}{{\text{m}}^{\text{3}}}{\text{ of liquid fuel}}}&{ = 2.7 \times {{10}^{10}}{\text{ J}}} \\ {{\text{Rate at which fuel is consumed}}}&{ = 0.13{\text{ g}}\,{{\text{s}}^{ - 1}}} \\ {{\text{Latent heat of vaporization of the fuel}}}&{ = 290{\text{ kJ}}\,{\text{k}}{{\text{g}}^{ - 1}}} \end{array}\]
Define electric field strength.
A thundercloud can be modelled as a negatively charged plate that is parallel to the ground.
The magnitude of the charge on the plate increases due to processes in the atmosphere. Eventually a current discharges from the thundercloud to the ground.
On the diagram, draw the electric field pattern between the thundercloud base and the ground.
(i) Determine the magnitude of the electric field between the base of the thundercloud and the ground.
(ii) State two assumptions made in (c)(i).
1.
2.
(iii) When the thundercloud discharges, the average discharge current is 1.8 kA. Estimate the discharge time.
(iv) The potential difference between the thundercloud and the ground before discharge is \(2.5 \times {10^8}{\text{ V}}\). Determine the energy released in the discharge.
Define the energy density of a fuel.
(i) Use the data to calculate the power output of the room heater, ignoring the power required to convert the liquid fuel into a gas.
(ii) Show why, in your calculation in (b)(i), the power required to convert the liquid fuel into a gas at its boiling point can be ignored.
State, in terms of molecular structure and their motion, two differences between a liquid and a gas.
1.
2.
Markscheme
force acting per unit charge;
on positive test / point charge;
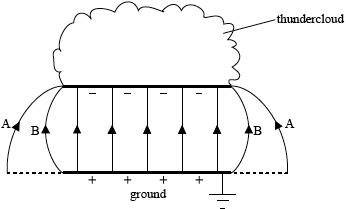
lines connecting plate and ground equally spaced in the central region of thundercloud and touching both plates; (judge by eye)
edge effects shown; (accept either edge effect A or B shown on diagram)
field direction correct;
(i) \(\sigma = \left( {\frac{{35}}{{1.2 \times {{10}^7}}} = } \right){\text{ }}2.917 \times {10^{ - 6}}{\text{ (C}}\,{{\text{m}}^{ - 2}})\);
\(E = \frac{{2.917 \times {{10}^{ - 6}}}}{{8.85 \times {{10}^{ - 12}}}}\);
\( = 3.3 \times {10^5}{\text{ N}}\,{{\text{C}}^{ - 1}}\) or \({\text{V}}\,{{\text{m}}^{ - 1}}\);
Award [3] for bald correct answer.
(ii) edge of thundercloud parallel to ground;
thundercloud and ground effectively of infinite length;
permittivity of air same as vacuum;
(iii) \(t = \frac{Q}{I}\);
\(t = \frac{{35}}{{1800}}\);
\( = 20{\text{ m}}\,{\text{s}}\);
(iv) use of energy \( = {\text{p.d.}} \times {\text{charge}}\);
\({\text{average p.d.}} = 1.25 \times {10^8}{\text{ (V)}}\);
\({\text{energy released}} = 1.25 \times {10^8} \times 35\);
\( = 4.4 \times {10^9}{\text{ J}}\);
Award [3 max] for 8.8 GJ if average p.d. point omitted.
Accept solution which uses average current \(\left( {from \frac{{charge}}{{time}}} \right)\).
Allow ecf from (c)(ii).
energy (released) per unit mass;
Accept per unit volume or per kg or per m3.
Do not accept per unit density.
(i) volume of fuel used per second \( = \frac{{{\text{rate}}}}{{{\text{density}}}}{\text{ }}\left( { = {\text{1.63}} \times {\text{1}}{{\text{0}}^{ - 7}}{\text{ (}}{{\text{m}}^{\text{3}}})} \right)\);
\({\text{energy}} = 2.7 \times {10^{10}} \times 1.63 \times {10^{ - 7}}\);
\( = (4.3875 = ){\text{ }}4.4{\text{ kW}}\);
Award [3] for bald correct answer.
(ii) power required \( = (2.9 \times {10^5} \times 0.13 \times {10^{ - 3}} = ){\text{ }}38{\text{ W}}\);
small fraction/less than 1% of overall power output / OWTTE;
sensible comment comparing molecular structure;
e.g. liquid molecular structure (more) ordered than that of a gas.
in gas molecules far apart/about 10 molecular spacings apart / in liquid molecules close/touching.
sensible comment comparing motion of molecules;
e.g. in liquid: molecules interchange places with neighbouring molecules / no long
distance motion.
in gases: no long-range order / long distance motion.
Examiners report
Many omitted the reference to a test charge that is positive.
Common errors were to draw the field lines in the wrong direction, to omit edge effects, and to fail to draw field lines that touch the plates.
(i) This part was well done.
(ii) Most candidates could only identify one assumption made in the calculation.
(iii) The estimation of discharge time was well done.
(iv) There was a general failure to recognise that the average pd during the discharge is half the maximum (starting) value and this lost a mark.
A handful of candidates defined energy density as energy converted per unit density, but most gave energy released per unit mass with a minority quoting energy released per unit volume.
(i) Again, this was done well by the majority with the usual smattering of significant figure penalties and mistakes in handling powers of ten.
(ii) Arguments were weak and poorly supported by calculation.
Candidates found great difficulty in stating the differences between liquids and gases. They often focused on either molecular structure or motion, but not both as required in the question.

