| Date | November 2009 | Marks available | 1 | Reference code | 09N.2.hl.TZ0.7 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Suggest | Question number | 7 | Adapted from | N/A |
Question
The Born-Haber cycle for MgO under standard conditions is shown below.
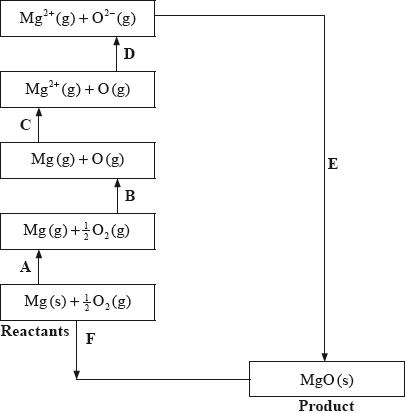
The values are shown in the table below.
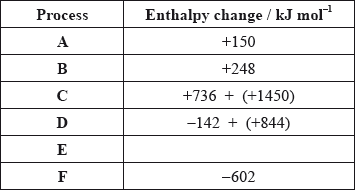
Identify the processes represented by A, B and D in the cycle.
Define the enthalpy change, F.
Determine the value of the enthalpy change, E.
Define the enthalpy change C for the first value. Explain why the second value is significantly larger than the first.
The inter-ionic distance between the ions in NaF is very similar to that between the ions in MgO. Suggest with a reason, which compound has the higher lattice enthalpy value.
The standard enthalpy change of three combustion reactions is given below in kJ.
\[\begin{array}{*{20}{l}} {{\text{2}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{6}}}{\text{(g)}} + {\text{7}}{{\text{O}}_{\text{2}}}{\text{(g)}} \to {\text{4C}}{{\text{O}}_{\text{2}}}{\text{(g)}} + {\text{6}}{{\text{H}}_{\text{2}}}{\text{O(l)}}}&{\Delta {H^\Theta } = - 3120} \\ {{\text{2}}{{\text{H}}_2}({\text{g)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{2}}{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = - {\text{572}}} \\ {{{\text{C}}_2}{{\text{H}}_4}({\text{g)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}} + 2{{\text{H}}_2}{\text{O(l)}}}&{\Delta {H^\Theta } = - {\text{1411}}} \end{array}\]
Based on the above information, calculate the standard change in enthalpy, \(\Delta {H^\Theta }\), for the following reaction.
\[{{\text{C}}_2}{{\text{H}}_6}({\text{g)}} \to {{\text{C}}_2}{{\text{H}}_4}({\text{g)}} + {{\text{H}}_2}{\text{(g)}}\]
Predict, stating a reason, whether the sign of \({\Delta {S^\Theta }}\) for the above reaction would be positive or negative.
Discuss why the above reaction is non-spontaneous at low temperature but becomes spontaneous at high temperatures.
Using bond enthalpy values, calculate \(\Delta {H^\Theta }\) for the following reaction.
\[{{\text{C}}_2}{{\text{H}}_6}({\text{g)}} \to {{\text{C}}_2}{{\text{H}}_4}({\text{g)}} + {{\text{H}}_2}{\text{(g)}}\]
Suggest with a reason, why the values obtained in parts (b) (i) and (b) (iv) are different.
Markscheme
A: sublimation/atomization;
B: atomization/half dissociation enthalpy;
D: (sum of 1st and 2nd) electron affinity;
Do not accept vaporization for A and B.
Accept \(\Delta {H_{AT}}\)\( \cdot \) or \(\Delta {H_{EA}}\).
enthalpy change when one mole of the compound is formed from its elements (in their standard states);
under standard conditions / 25 °C/298 K and 1 atm/\({\text{101.3 kPa/1.01}} \times {\text{105 Pa}}\);
\( - 602 = 150 + 248 + 2186 + 702 + E\);
\( - {\text{3888 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Do not allow 3889 (given in data booklet).
Allow 3888 (i.e no minus sign).
Award [2] for the correct final answer.
energy required to remove one electron;
from an atom in its gaseous state;
electron removed from a positive ion;
decrease in electron-electron repulsion / increase in nucleus-electron attraction;
MgO;
double ionic charge / both ions carry +2 and –2 charge/greater charge compared to +1 and –1;
\[\begin{array}{*{20}{l}} {\left( {{{\text{C}}_2}{{\text{H}}_6}{\text{(g)}} + {\text{3}}\frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {\text{2C}}{{\text{O}}_2}{\text{(g)}} + {\text{3}}{{\text{H}}_2}{\text{O(l)}}} \right)}&{\Delta {H^\Theta } = - {\text{1560;}}} \\ {\left( {{{\text{H}}_2}{\text{O(l)}} \to {{\text{H}}_2}{\text{(g)}} + \frac{1}{2}{{\text{O}}_2}{\text{(g)}}} \right)}&{\Delta {H^\Theta } = + {\text{286;}}} \\ {\left( {{\text{2C}}{{\text{O}}_2}{\text{(g)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}} \to {{\text{C}}_2}{{\text{H}}_4}{\text{(g)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}}} \right)}&{\Delta {H^\Theta } = + {\text{1411;}}} \\ {\left( {{{\text{C}}_2}{{\text{H}}_6}{\text{(g)}} \to {{\text{C}}_2}{{\text{H}}_4}{\text{(g)}} + {{\text{H}}_2}{\text{(g)}}} \right)}&{\Delta {H^\Theta } = + {\text{137 (kJ);}}} \end{array}\]
Allow other correct methods.
Award [2] for –137.
Allow ECF for the final marking point.
positive;
increase in number of moles of gas;
at low temperature, \({\Delta {H^\Theta }}\) is positive and \({\Delta G}\) is positive;
at high temperature, factor \({\text{T}}\Delta {S^\Theta }\) predominates and \({\Delta G}\) is negative;
Bonds broken (1C–C, 6C–H, or 1C–C, 2C–H) = 2825/1173;
Bonds made (1C=C, 1H–H, 4C–H) = 2700/1048;
+125 (kJ);
Allow 125 but not –125 (kJ ) for the final mark.
Award [3] for the correct final answer.
bond enthalpy values are average values;
Examiners report
This was the second most popular question and in general candidates demonstrated a good understanding of the Born Haber cycle. Some candidates identified the process A as vaporization instead of atomization.
Most candidates correctly stated the definition of enthalpy change of formation although some omitted to specify the standard conditions.
The majority of candidates correctly calculated the lattice enthalpy value.
The definition of the first ionization energy was stated correctly by most candidates but in a few cases the term gaseous state was missing.
The compound with higher lattice enthalpy was correctly identified including the reason.
The majority of candidates manipulated the thermo-chemical equations and calculated the correct answer of +137 kJ although some reversed the sign.
The explanation for why the reaction was non-spontaneous at low temperature but became spontaneous at high temperature was not always precise and deprived many candidates of at least one mark.
The bond enthalpy calculation had the usual mistakes of using the wrong value from the data booklet, bond making minus bond breaking and –125 kJ instead of +125 kJ.

