| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.sl.TZ2.1 |
| Level | SL | Paper | 2 | Time zone | TZ2 |
| Command term | Calculate | Question number | 1 | Adapted from | N/A |
Question
If white anhydrous copper(II) sulfate powder is left in the atmosphere it slowly absorbs water vapour giving the blue pentahydrated solid.
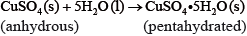
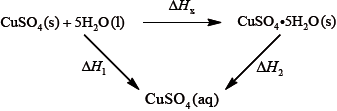
It is difficult to measure the enthalpy change for this reaction directly. However, it is possible to measure the heat changes directly when both anhydrous and pentahydrated copper(II) sulfate are separately dissolved in water, and then use an energy cycle to determine the required enthalpy change value, \(\Delta {H_{\text{x}}}\), indirectly.
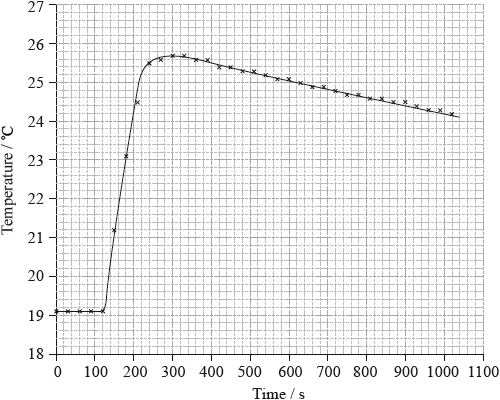
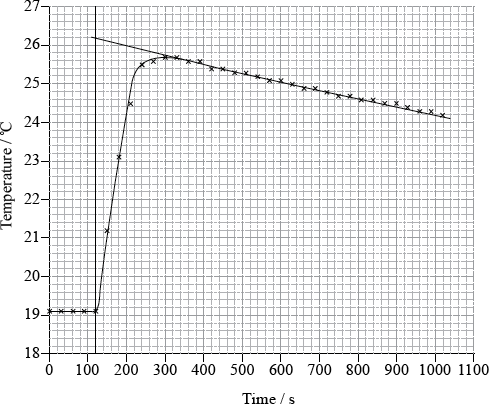
To determine \(\Delta {H_1}\) a student placed 50.0 g of water in a cup made of expanded polystyrene and used a data logger to measure the temperature. After two minutes she dissolved 3.99 g of anhydrous copper(II) sulfate in the water and continued to record the temperature while continuously stirring. She obtained the following results.
To determine \(\Delta {H_2}\), 6.24 g of pentahydrated copper(II) sulfate was dissolved in 47.75 g of water. It was observed that the temperature of the solution decreased by 1.10 °C.
The magnitude (the value without the \( + \) or \( - \) sign) found in a data book for \(\Delta {H_{\text{x}}}\) is \({\text{78.0 kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\).
Calculate the amount, in mol, of anhydrous copper(II) sulfate dissolved in the 50.0 g of water.
Determine what the temperature rise would have been, in °C, if no heat had been lost to the surroundings.
Calculate the heat change, in kJ, when 3.99 g of anhydrous copper(II) sulfate is dissolved in the water.
Determine the value of \(\Delta {H_1}{\text{ in kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\).
Calculate the amount, in mol, of water in 6.24 g of pentahydrated copper(II) sulfate.
Determine the value of \(\Delta {H_2}\) in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\).
Using the values obtained for \(\Delta {H_1}\) in (a) (iv) and \(\Delta {H_2}\) in (b) (ii), determine the value for \(\Delta {H_{\text{x}}}\) in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\).
Calculate the percentage error obtained in this experiment. (If you did not obtain an answer for the experimental value of \(\Delta {H_{\text{x}}}\) then use the value \({\text{70.0 kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), but this is not the true value.)
The student recorded in her qualitative data that the anhydrous copper(II) sulfate she used was pale blue rather than completely white. Suggest a reason why it might have had this pale blue colour and deduce how this would have affected the value she obtained for \(\Delta {H_{\text{x}}}\).
Markscheme
\({\text{amount}} = \frac{{3.99}}{{159.61}} = 0.0250{\text{ (mol)}}\);
26.1 (°C);
Accept answers between 26.0 and 26.2 ( °C).
temperature rise \( = 26.1 - 19.1 = 7.0\) (°C);
Accept answers between 6.9 °C and (7.1 °C) .
Award [2] for the correct final answer.
No ECF if both initial and final temperatures incorrect.
heat change \( = \frac{{50.0}}{{1000}} \times 4.18 \times 7.0/50.0 \times 4.18 \times 7.0\);
Accept 53.99 instead of 50.0 for mass.
\( = 1.5{\text{ (kJ)}}\);
Allow 1.6 (kJ) if mass of 53.99 is used.
Ignore sign.
\(\Delta {H_1} = \frac{{1.5}}{{0.0250}} = - 60{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Value must be negative to award mark.
Accept answers in range –58.0 to –60.0.
Allow –63 (kJ\(\,\)mol–1) if 53.99 g is used in (iii).
\({\text{(amount of CuS}}{{\text{O}}_4} \bullet {\text{5}}{{\text{H}}_{\text{2}}}{\text{O}} = \frac{{6.24}}{{249.71}} = {\text{) 0.0250 (mol)}}\);
\({\text{(amount of }}{{\text{H}}_{\text{2}}}{\text{O in 0.0250 mol of CuS}}{{\text{O}}_{\text{4}}} \bullet {\text{5}}{{\text{H}}_{\text{2}}}{\text{O}} = 5 \times 0.0250 = {\text{) 0.125 (mol)}}\).
\((50.0 \times 4.18 \times 1.10 = ){\text{ }}230{\text{ (J)}}\);
\(\left( {\frac{{229.9}}{{(1000{\text{ }}0.0250)}} = } \right){\text{ }} + 9.20{\text{ (kJ)}}\);
Accept mass of 47.75 or 53.99 instead of 50.00 giving answers of +.8.78 or +9.9.
Do not penalize missing + sign but penalize – sign unless charge already penalized in (a) (iv).
\(\left( {\Delta {H_{\text{x}}} = \Delta {H_2} - \Delta {H_2} = - 58.4 - ( + 9.20) = } \right){\text{ }} - 67.6{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\)
\(\frac{{[ - 78.0 - ( - 67.6)]}}{{ - 78.0}} \times 100 = 13.3\% \);
If 70.0 kJ\(\,\)mol−1 is used accept 10.3%.
the anhydrous copper(II) sulfate had already absorbed some water from the air / OWTTE;
the value would be less exothermic/less negative than expected as the temperature increase would be lower / less heat will be evolved when the anhydrous salt is dissolved in water / OWTTE;
Do not accept less without a reason.
Examiners report
Question 1 was a generally difficult question for candidates, but most students did pick up marks thanks to the application of error carried forward (ecf). In part (a) students could usually calculate the moles of anhydrous copper sulphate.
Very few candidates could correctly extrapolate the graph to calculate a temperature rise of 7.0 ºC.
Calculating using \({\text{q}} = {\text{mc}}\Delta {\text{T}}\) also caused problems as many students used the mass of the copper sulphate instead of the mass of water, and some also added 273 to the temperature change. Many candidates also forgot to convert to kJ.
The last part of this question required the calculation of \(\Delta H\), here many students forgot the – symbol to indicate it was exothermic and so did not gain the mark.
In part (b) the problems were similar as students used incorrect values in their calculation but were able to obtain some marks by error carried forward.
In part (b) the problems were similar as students used incorrect values in their calculation but were able to obtain some marks by error carried forward.
In part (b) the problems were similar as students used incorrect values in their calculation but were able to obtain some marks by error carried forward.
In part (c) many could calculate the % error and apply Hess’s law to calculate \(\Delta H\). Throughout this question there were numerous instances of students using an incorrect number of significant figures and this led to another mark being lost.

