| Date | May 2016 | Marks available | 5 | Reference code | 16M.2.hl.TZ0.4 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Hence and Sketch | Question number | 4 | Adapted from | N/A |
Question
Consider the differential equation \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{x}{y}\), where \(y \ne 0\).
Find the general solution of the differential equation, expressing your answer in the form \(f(x,{\text{ }}y) = c\), where \(c\) is a constant.
(i) Hence find the particular solution passing through the points \((1,{\rm{ \pm }}\sqrt 2 )\).
(ii) Sketch the graph of your solution and name the type of curve represented.
(i) Write down the particular solution passing through the points \((1,{\text{ }} \pm 1)\).
(ii) Give a geometrical interpretation of this solution in relation to part (b).
(i) Find the general solution of the differential equation \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{x}{y} + \frac{y}{x}\), where \(xy \ne 0\).
(ii) Find the particular solution passing through the point \((1,{\text{ }}\sqrt 2 )\).
(iii) Sketch the particular solution.
(iv) The graph of the solution only contains points with \(\left| x \right| > a\).
Find the exact value of \(a,{\text{ }}a > 0\).
Markscheme
attempt to separate the variables M1
\(\int {y\frac{{{\text{d}}y}}{{{\text{d}}x}}{\text{d}}x = \int {x{\text{d}}x} } \) A1
Note: Accept \(\int {y{\text{d}}y = \int {x{\text{d}}x} } \).
obtain \(\frac{1}{2}{y^2} = \frac{1}{2}{x^2} + {\text{ constant }}( \Rightarrow {y^2} - {x^2} = c)\) A1
[3 marks]
(i) substitute the coordinates for both points M1
\({( \pm \sqrt 2 )^2} - {1^2} = 1\)
obtain \({y^2} - {x^2} = 1\) or equivalent A1
(ii) 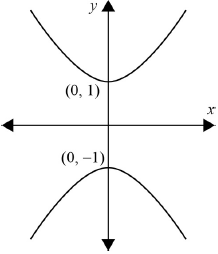 A1A1
A1A1
Note: A1 for general shape including two branches and symmetry;
A1 for values of the intercepts.
(rectangular) hyperbola A1
[5 marks]
(i) \({y^2} - {x^2} = 0\) A1
(ii) the two straight lines \(y = \pm x\) A1
form the asymptotes to the hyperbola found above, or equivalent A1
[3 marks]
(i) the equation is homogeneous, so attempt to substitute \(y = vx\) M1
as a first step write \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = x\frac{{{\text{d}}v}}{{{\text{d}}x}} + v\) (A1)
then \(x\frac{{{\text{d}}v}}{{{\text{d}}x}} + v = \frac{1}{v} + v\) A1
attempt to solve the resulting separable equation M1
\(\int {v{\text{d}}v = \int {\frac{1}{x}{\text{d}}x} } \) A1
obtain \(\frac{1}{2}{v^2} = \ln \left| x \right| + {\text{ constant}} \Rightarrow {y^2} = 2{x^2}\ln \left| x \right| + c{x^2}\) A1
(ii) substituting the coordinates (M1)
obtain \(c = 2 \Rightarrow {y^2} = 2{x^2}\ln \left| x \right| + 2{x^2}\) A1
(iii) 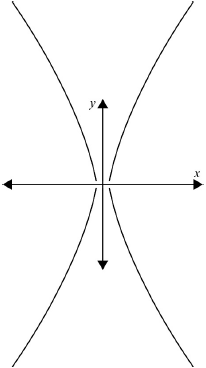 A1
A1
(iv) since \({y^2} > 0\) and \({x^2} \ne 0\) R1
\(\ln \left| x \right| > - 1 \Rightarrow \left| x \right| > {{\text{e}}^{ - 1}}\) A1
\(a = {{\text{e}}^{ - 1}}\) A1
Note: The R1 may be awarded for a correct reason leading to subsequent correct work.
[12 marks]
Examiners report
Although (a), (b) and (c) were generally well done, it was rare to see a completely satisfactory geometrical answer to part (c)(ii). A few candidates solved the differential equation as a homogeneous equation.
Although (a), (b) and (c) were generally well done, it was rare to see a completely satisfactory geometrical answer to part (c)(ii). A few candidates solved the differential equation as a homogeneous equation.
Although (a), (b) and (c) were generally well done, it was rare to see a completely satisfactory geometrical answer to part (c)(ii). A few candidates solved the differential equation as a homogeneous equation.
For part (d) most candidates used the correct solution method for a homogeneous differential equation. A few found the algebra hard going in finding the particular solution. Most approaches to the final part were unsatisfactory, with a lack of proper consideration of the inequalities in the question.

