| Date | May 2012 | Marks available | 24 | Reference code | 12M.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
(i) Show that \(\frac{{\rm{d}}}{{{\rm{d}}\theta }}(\sec \theta \tan \theta + \ln (\sec \theta + \tan \theta )) = 2{\sec ^3}\theta \) .
(ii) Hence write down \(\int {{{\sec }^3}\theta {\rm{d}}\theta } \) .
Consider the differential equation \((1 + {x^2})\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + xy = 1 + {x^2}\) given that \(y = 1\) when \(x = 0\) .
(i) Use Euler’s method with a step length of \(0.1\) to find an approximate value for y when \(x = 0.3\) .
(ii) Find an integrating factor for determining the exact solution of the differential equation.
(iii) Find the solution of the equation in the form \(y = f(x)\) .
(iv) To how many significant figures does the approximation found in part (i) agree with the exact value of \(y\) when \(x = 0.3\) ?
Markscheme
(i) \(\frac{{\rm{d}}}{{{\rm{d}}\theta }}(\sec \theta \tan \theta + \ln (\sec \theta + \tan \theta ))\)
\( = {\sec ^3}\theta + \sec \theta {\tan ^2}\theta + \frac{{\sec \theta \tan \theta + {{\sec }^2}\theta }}{{\sec \theta + \tan \theta }}\) M1A1A1
Note: Award M1 for a valid attempt to differentiate either term.
\( = {\sec ^3}\theta + \sec \theta ({\sec ^2}\theta - 1) + \sec \theta \) A1
\( = 2{\sec ^3}\theta \) AG
(ii) \(\int {{{\sec }^3}\theta {\rm{d}}\theta } = \frac{1}{2}(\sec \theta \tan \theta + \ln (\sec \theta + \tan \theta ))( + C)\) A1
[5 marks]
(i) \(\frac{{{\rm{d}}y}}{{{\rm{d}}x}} = 1 - \frac{{xy}}{{1 + {x^2}}}\) A1
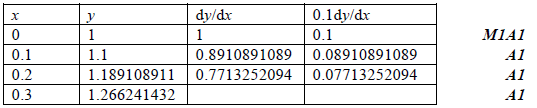
Note: Accept tabular values correct to 3 significant figures.
\(y \approx 1.27\) when \(x = 0.3\) A1
(ii) consider the equation in the form
\(\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \frac{{xy}}{{1 + {x^2}}} = 1\) (M1)
the integrating factor I is given by
\(I = \exp \int {\left( {\frac{x}{{1 + {x^2}}}} \right)} {\rm{d}}x\) A1
\( = \exp \left( {\frac{1}{2}\ln (1 + {x^2})} \right)\) A1
\( = \sqrt {1 + {x^2}} \) A1
Note: Accept also the fact that the integrating factor for the original equation is \(\frac{1}{{\sqrt {1 + {x^2}} }}\) .
(iii) consider the equation in the form
\(\sqrt {1 + {x^2}} \frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \frac{{xy}}{{\sqrt {1 + {x^2}} }} = \sqrt {1 + {x^2}} \) (M1)
integrating,
\(y\sqrt {1 + {x^2}} = \int {\sqrt {1 + {x^2}} {\rm{d}}x} \) A1
to integrate the right hand side, put \(x = \tan \theta \) , \({\rm{d}}x = {\sec ^2}\theta {\rm{d}}\theta \) M1A1
\(\int {\sqrt {1 + {x^2}} } {\rm{d}}x = \int {\sqrt {1 + {{\tan }^2}\theta } } .{\sec ^2}\theta {\rm{d}}\theta \) A1
\( = \int {{{\sec }^3}\theta {\rm{d}}\theta } \) A1
\( = \frac{1}{2}(\sec \theta \tan \theta + \ln (\sec \theta + \tan \theta ))\)
\( = \frac{1}{2}\left( {x\sqrt {1 + {x^2}} + \ln (x + \sqrt {1 + {x^2}} )} \right)\) A1
the solution to the differential equation is therefore
\(y\sqrt {1 + {x^2}} = \frac{1}{2}\left( {x\sqrt {1 + {x^2}} + \ln \left( {x + \sqrt {1 + {x^2}} } \right)} \right) + C\) A1
Note: Do not penalize the omission of C at this stage.
\(y = 1\) when \(x = 0\) gives \(C = 1\) M1A1
the solution is \(y = \frac{1}{{2\sqrt {1 + {x^2}} }}\left( {x\sqrt {1 + {x^2}} + \ln \left( {x + \sqrt {1 + {x^2}} } \right)} \right) + \frac{1}{{\sqrt {1 + {x^2}} }}\) A1
(iv) when \(x = 0.3\) , \(y = 1.249 \ldots \) A1
the approximation is only correct to 1 significant figure A1
[24 marks]
Examiners report
Most candidates managed to solve (a) successfully although some solutions required a page or more to complete with candidates rewriting \(\sec \theta \) and \(\tan \theta \) in terms of \(\sin \theta \) and \(\cos \theta \) which increased the complexity of the problem and sometimes led to algebraic errors.
Most candidates made a good attempt at (b) (i), those candidates who gave their solution in tabular form being most successful. In (b)(ii), most candidates found the correct integrating factor but many were unable to solve the differential equation in (b)(iii) with some failing to see that the result in (a) was intended as a hint for an appropriate substitution.

