| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.sl.TZ2.5 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show that | Question number | 5 | Adapted from | N/A |
Question
Violeta plans to grow flowers in a rectangular plot. She places a fence to mark out the perimeter of the plot and uses 200 metres of fence. The length of the plot is \(x\) metres.
Violeta places the fence so that the area of the plot is maximized.
By selling her flowers, Violeta earns 2 Bulgarian Levs (BGN) per square metre of the plot.
Violeta wants to invest her 5000 BGN.
A bank offers a nominal annual interest rate of 4%, compounded half-yearly.
Another bank offers an interest rate of \(r\)% compounded annually, that would allow her to double her money in 12 years.
Show that the width of the plot, in metres, is given by \(100 - x\).
Write down the area of the plot in terms of \(x\).
Find the value of \(x\) that maximizes the area of the plot.
Show that Violeta earns 5000 BGN from selling the flowers grown on the plot.
Find the amount of money that Violeta would have after 6 years. Give your answer correct to two decimal places.
Find how long it would take for the interest earned to be 2000 BGN.
Find the lowest possible value for \(r\).
Markscheme
\(\frac{{200 - 2x}}{2}\) (or equivalent) (M1)
OR
\(2x + 2y = 200\) (or equivalent) (M1)
Note: Award (M1) for a correct expression leading to \(100 - x\) (the \(100 - x\) does not need to be seen). The 200 must be seen for the (M1) to be awarded. Do not accept \(100 - x\) substituted in the perimeter of the rectangle formula.
\(100 - x\) (AG)
[1 mark]
\(({\text{area}} = ){\text{ }}x(100 - x)\)\(\,\,\,\)OR\(\,\,\,\)\( - {x^2} + 100x\) (or equivalent) (A1)
[1 mark]
\(x = \frac{{ - 100}}{{ - 2}}\)\(\,\,\,\)OR\(\,\,\,\)\( - 2x + 100 = 0\)\(\,\,\,\)OR\(\,\,\,\)graphical method (M1)
Note: Award (M1) for use of axis of symmetry formula or first derivative equated to zero or a sketch graph.
\(x = 50\) (A1)(ft)(G2)
Note: Follow through from part (b), provided x is positive and less than 100.
[2 marks]
\(50(100 - 50) \times 2\) (M1)(M1)
Note: Award (M1) for substituting their \(x\) into their formula for area (accept “\(50 \times 50\)” for the substituted formula), and (M1) for multiplying by 2. Award at most (M0)(M1) if their calculation does not lead to 5000 (BGN), although the 5000 (BGN) does not need to be seen explicitly.
Substitution of 50 into area formula may be seen in part (c).
5000 (BGN) (AG)
[2 marks]
\(5000{\left( {1 + \frac{4}{{2 \times 100}}} \right)^{2 \times 6}}\) (M1)(A1)
Note: Award (M1) for substitution into compound interest formula, (A1) for correct substitution.
OR
\({\text{N}} = 6\)
\({\text{I}}\% = 4\)
\({\text{PV}} = - 5000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for \({\text{C/Y}} = 2\) seen, (M1) for other correct entries.
OR
\({\text{N}} = 12\)
\({\text{I}}\% = 4\)
\({\text{PV}} = - 5000\)
\({\text{P/Y}} = 2\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for \({\text{C/Y}} = 2\) seen, (M1) for other correct entries.
6341.21 (BGN) (A1)(G3)
Note: Award (A1) for correct answer, to two decimal places only.
Award (G2) for 6341.20 or a correct, unrounded final answer if no working is seen (6341.2089…).
[3 marks]
\(5000{\left( {1 + \frac{4}{{2 \times 100}}} \right)^{2 \times t}} = 7000\) (M1)(A1)(ft)
Note: Award (M1) for using the compound interest formula with a variable for time, (A1)(ft) for substituting the correct values and equating to 7000. Follow through for their “2” from part (e)(i).
OR
\({\text{I% }} = 4\)
\({\text{PV}} = ( \pm )5000\)
\({\text{FV}} = \mp 7000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for 7000 seen, (M1) for the other correct entries.
Award (M1) for their C/Y from part (e)(i).
OR
\({\text{I% }} = 4\)
\({\text{PV}} = ( \pm )5000\)
\({\text{FV}} = \mp 7000\)
\({\text{P/Y}} = 2\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for 7000 seen, (M1) for the other correct entries.
Award (M1) for their C/Y from part (e)(i).
OR
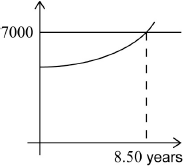(M1)(A1)(ft)
Note: Award (M1) for a sketch with a straight line intercepted by appropriate curve, (A1)(ft) for numerical answer in the range of 8.4 and 8.5.
Follow through from their part (e)(i).
\(t = 8.50{\text{ (years) }}(8.49564 \ldots )\) (A1)(ft)(G3)
Note: Award only (A1) if 16.9912… is seen without working. If working is seen, award at most (M1)(A1)(A0).
[3 marks]
\(5000{\left( {1 + \frac{r}{{100}}} \right)^{12}} = 10000\) (M1)
Note: Award (M1) for correct substitution into compound interest formula with 10 000 seen.
OR
\(2 = {\left( {1 + \frac{r}{{100}}} \right)^{12}}\) (M1)
Note: Award (M1) for correct substitution and simplification of compound interest formula, equating to 2.
\(r = 5.95{\text{ (% ) }}(5.94630 \ldots )\) (A1)(G2)
[2 marks]
