| Date | November 2014 | Marks available | 1 | Reference code | 14N.1.sl.TZ0.14 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Label and Mark | Question number | 14 | Adapted from | N/A |
Question
The axis of symmetry of the graph of a quadratic function has the equation x \( = - \frac{1}{2}\)
.
Draw the axis of symmetry on the following axes.
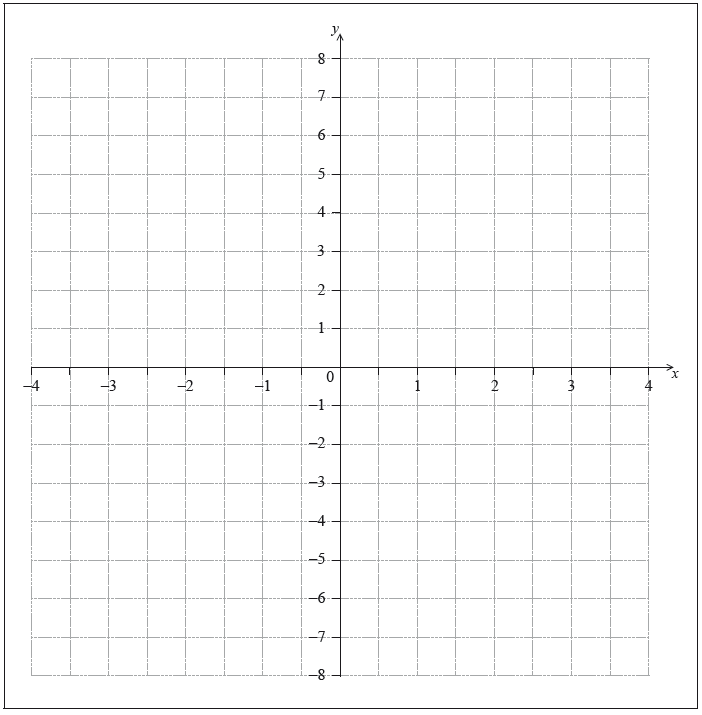
The graph of the quadratic function intersects the x-axis at the point N(2, 0) . There is a second point, M, at which the graph of the quadratic function intersects the x-axis.
Draw the axis of symmetry on the following axes.
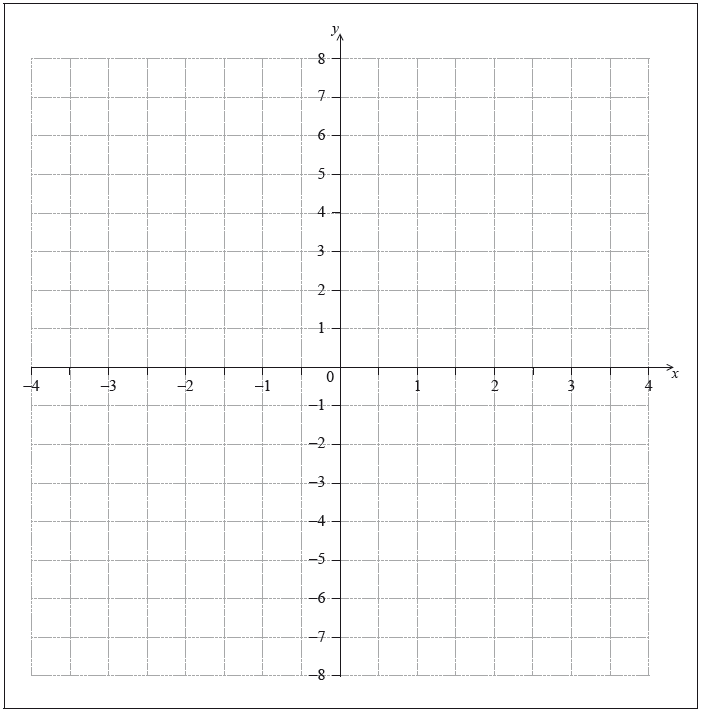
The graph of the quadratic function intersects the \(x\)-axis at the point \({\text{N}}(2, 0)\). There is a second point, \({\text{M}}\), at which the graph of the quadratic function intersects the \(x\)-axis.
Clearly mark and label point \({\text{M}}\) on the axes.
(i) Find the value of \(b\) and the value of \(c\).
(ii) Draw the graph of the function on the axes.
Markscheme
vertical straight line which may be dotted passing through \(\left( { - \frac{1}{2},{\text{ }}0} \right)\) (A1) (C1)
vertical straight line which may be dotted passing through \(\left( { - \frac{1}{2},{\text{ }}0} \right)\) (A1) (C1)
point \({\text{M }}( - 3,{\text{ }}0)\) correctly marked on the \(x\)-axis (A1)(ft) (C1)
Note: Follow through from part (a).
(i) \(b = 1\), \(c = - 6\) (A1)(ft)(A1)(ft)
Notes: Follow through from (b).
(ii) smooth parabola passing through \({\text{M}}\) and \({\text{N}}\) (A1)(ft)
Note: Follow through from their point \({\text{M}}\) from part (b).
parabola passing through \((0,{\text{ }} - 6)\) and symmetrical about \(x = - 0.5\) (A1)(ft) (C4)
Note: Follow through from part (c)(i).
If parabola is not smooth and not concave up award at most (A1)(A0).

