| Date | May 2017 | Marks available | 6 | Reference code | 17M.1.sl.TZ2.15 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 15 | Adapted from | N/A |
Question
Consider the following graphs of quadratic functions.
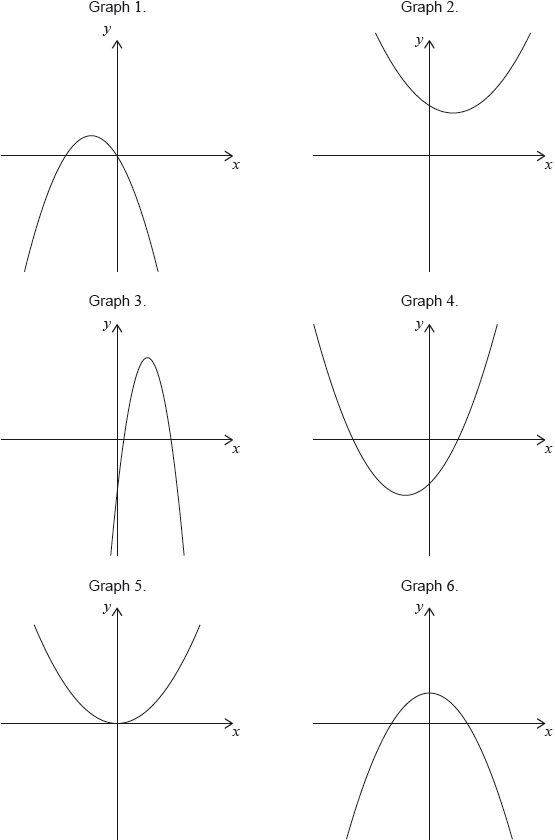
The equation of each of the quadratic functions can be written in the form \(y = a{x^2} + bx + c\), where \(a \ne 0\).
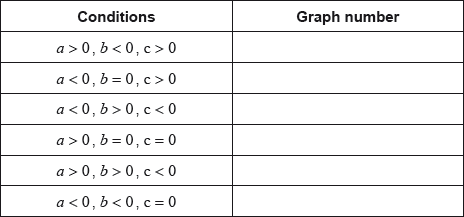
Each of the sets of conditions for the constants \(a\), \(b\) and \(c\), in the table below, corresponds to one of the graphs above.
Write down the number of the corresponding graph next to each set of conditions.
Markscheme
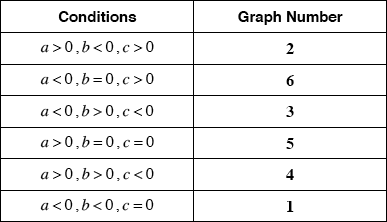(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each correct entry.
[6 marks]
Examiners report
[N/A]
Syllabus sections
Show 102 related questions
- 18M.1.sl.TZ2.14c: Find the x-coordinate of the point at which the normal to the graph of f has...
- 18M.1.sl.TZ2.14b: Find the gradient of the graph of f at \(x = - \frac{1}{2}\).
- 18M.1.sl.TZ2.14a: Find f'(x)
- 18M.1.sl.TZ2.13c: Find the number of shirts produced when the cost of production is lowest.
- 18M.1.sl.TZ2.13b: Find the value of s.
- 18M.1.sl.TZ2.13a: Find the cost of producing 70 shirts.
- 18M.1.sl.TZ1.12d: The graph intersects the x-axis at a second point, P. Find the x-coordinate of P.
- 18M.1.sl.TZ1.12c: Hence find the value of a and of b.
- 18M.1.sl.TZ1.12a: Using only this information, write down an equation in terms of a and b.
- 18M.1.sl.TZ1.12b: Using this information, write down a second equation in terms of a and b.
- 17N.1.sl.TZ0.15d: Find the price, \(p\), that will give Maria the highest weekly profit.
- 17N.1.sl.TZ0.15c: Write down an expression for \(W\) in terms of \(p\).
- 17N.1.sl.TZ0.15b: Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of...
- 17N.1.sl.TZ0.15a: Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of...
- 17N.1.sl.TZ0.11c: Find the value of \(a\) and of \(b\).
- 17N.1.sl.TZ0.11b: Write down the value of \(c\).
- 17N.1.sl.TZ0.11a: Find the equation of the axis of symmetry of the graph of \(y = f(x)\).
- 16N.2.sl.TZ0.3f: Write down the length of MD correct to five significant figures.
- 17M.2.sl.TZ2.5f: Find the lowest possible value for \(r\).
- 17M.2.sl.TZ2.5e.ii: Find how long it would take for the interest earned to be 2000 BGN.
- 17M.2.sl.TZ2.5e.i: Find the amount of money that Violeta would have after 6 years. Give your answer correct to...
- 17M.2.sl.TZ2.5d: Show that Violeta earns 5000 BGN from selling the flowers grown on the plot.
- 17M.2.sl.TZ2.5c: Find the value of \(x\) that maximizes the area of the plot.
- 17M.2.sl.TZ2.5b: Write down the area of the plot in terms of \(x\).
- 17M.2.sl.TZ2.5a: Show that the width of the plot, in metres, is given by \(100 - x\).
- 17M.2.sl.TZ1.6e: Find the \(y\)-coordinate of the local minimum.
- 17M.2.sl.TZ1.6d.ii: Hence justify that \(g\) is decreasing at \(x = - 1\).
- 17M.2.sl.TZ1.6d.i: Find \(g’( - 1)\).
- 17M.2.sl.TZ1.6c: Use your answer to part (a) and the value of \(k\), to find the \(x\)-coordinates of the...
- 17M.2.sl.TZ1.6b.ii: Find the equation of the tangent to the graph of \(y = g(x)\) at \(x = 2\). Give your answer...
- 17M.2.sl.TZ1.6b.i: Show that \(k = 6\).
- 17M.2.sl.TZ1.6a: Find \(g'(x)\).
- 17M.1.sl.TZ1.15c: Write down the second \(x\)-intercept of the function.
- 17M.1.sl.TZ1.15b: Find the value of \(a\) and of \(b\).
- 17M.1.sl.TZ1.15a: Write down the value of \(c\).
- 16M.2.sl.TZ1.3f: The nearest coastguard can see the flare when its height is more than \(40\) metres above sea...
- 16M.2.sl.TZ1.3e: i) Show that the flare reached its maximum height \(40\) seconds after being fired. ii)...
- 16M.2.sl.TZ1.3d: Find \(h'\,(t)\,.\)
- 16M.2.sl.TZ1.3c: The flare fell into the sea \(k\) seconds after it was fired. Find the value of \(k\) .
- 16M.2.sl.TZ1.3b: Find the height of the flare \(15\) seconds after it was fired.
- 16M.2.sl.TZ1.3a: A distress flare is fired into the air from a ship at sea. The height, \(h\) , in metres, of...
- 16M.1.sl.TZ1.11c: Find the value of \(c\) .
- 16M.1.sl.TZ1.11b: Point \({\text{A}}( - 2,\,5)\) lies on the graph of \(y = f(x)\) . The gradient of the...
- 16M.1.sl.TZ1.11a: Consider the function \(f(x) = a{x^2} + c\). Find \(f'(x)\)
- 10M.1.sl.TZ1.14c: Calculate the x-coordinate of the vertex of the graph of f (x).
- 10M.1.sl.TZ2.13b: The axis of symmetry is x = 2.5. Find the value of r.
- 10M.1.sl.TZ2.13c: The axis of symmetry is x = 2.5. Write down the minimum value of y.
- 10M.1.sl.TZ2.13a: Write down the value of q.
- 10N.1.sl.TZ0.10b: Write down the equation of the axis of symmetry of the graph of f (x).
- 10N.1.sl.TZ0.10c: The equation f (x) = 12 has two solutions. One of these solutions is x = 6. Use the symmetry...
- 10N.1.sl.TZ0.10d: The minimum value for y is – 4. Write down the range of f (x).
- 10N.1.sl.TZ0.10a: Write down the solutions to the equation f (x) = 0.
- 11N.1.sl.TZ0.13a: (i) Find the value of \(k\) . (ii) Calculate the \(y\)-coordinate of this minimum point.
- 11N.1.sl.TZ0.13b: Sketch the graph of \(y = f(x)\) for the domain \( - 1 \leqslant x \leqslant 3\).
- 12N.1.sl.TZ0.10b: Find the equation of the axis of symmetry of the graph of y = f (x) .
- 12N.1.sl.TZ0.10a: It is given that f (2) = −5 . Find the value of a .
- 12M.1.sl.TZ1.4a: Write down the equation of the axis of symmetry.
- 12M.1.sl.TZ1.4c: The graph of y = f (x) intersects the x-axis for a second time at point D. Write down the...
- 12M.1.sl.TZ2.11a: Find the value of (i) b ; (ii) c .
- 12M.1.sl.TZ2.11b: The domain of f is 0 ≤ x ≤ 6. Find the range of f .
- 09N.1.sl.TZ0.13b: Given that the quadratic function has an equation \(y = -x^2 + bx + c\) where...
- 09N.1.sl.TZ0.13a: Calculate the value of p.
- 09N.2.sl.TZ0.5A, e: Write down the maximum value of the function f (x) = 3 + 2x − x2.
- 09N.2.sl.TZ0.5A, c: On the same axes sketch the graph of y = 3 + 2x − x2. Indicate clearly where this curve...
- 09N.2.sl.TZ0.5B, a: The curve y = px2 + qx − 4 passes through the point (2, –10). Use the above information to...
- 11M.1.sl.TZ1.6b: Another point, C , which lies on the graph of \(y = f(x)\) has the same \(y\)-coordinate as A...
- 09M.1.sl.TZ1.7a: Write down the equation of the axis of symmetry.
- 11M.1.sl.TZ1.6a: Find the coordinates of B .
- 09M.1.sl.TZ1.7b: Write down the coordinates of the minimum point.
- 09M.1.sl.TZ2.14a: Find the value of h.
- 09M.1.sl.TZ2.14b: Find the equation of the curve.
- 13M.1.sl.TZ1.9a: Write down the value of c.
- 13M.1.sl.TZ1.9b: Find the value of b.
- 13M.1.sl.TZ1.9c: Find the x-intercepts of the graph of f .
- 13M.1.sl.TZ1.9d: Write down \(f (x)\) in the form \(f (x) = −(x − p) (x + q)\).
- 13M.2.sl.TZ2.5a: The coordinates of point A are (75, 450). Determine whether point A is on the bicycle track....
- SPM.1.sl.TZ0.15a: Find \(P(x)\) .
- 07M.2.sl.TZ0.3ii.a: Using your graphic display calculator or otherwise, find the value of a.
- 07N.2.sl.TZ0.5f: State the equation of the axis of symmetry of P.
- 07N.2.sl.TZ0.5g: Find the coordinates of the vertex of P and state the gradient of the curve at this point.
- 07N.1.sl.TZ0.5: The following curves are sketches of the graphs of the functions given below, but in a...
- 08N.1.sl.TZ0.13c: The diagram below shows the graph of the function \(f(x) = {x^2} - kx\) for a particular...
- 08N.1.sl.TZ0.13d: The diagram below shows the graph of the function \(f(x) = {x^2} - kx\) for a particular...
- 08M.2.sl.TZ1.5i.d: Consider a function \(f(x) = 3{x^2} + 13x - 10\) . Calculate the minimum value of this...
- 08M.2.sl.TZ1.5i.c: Consider a function \(f(x) = 3{x^2} + 13x - 10\) . Find the equation of the axis of symmetry...
- 14M.2.sl.TZ2.6a: Write down the value of \(c\).
- 14M.2.sl.TZ2.6b: Find the value of \(a\).
- 14M.2.sl.TZ2.6c: Hence write down the equation of the quadratic function which models the edge of the water tank.
- 14M.2.sl.TZ2.6e: The water tank is shown below. It is partially filled with water. State what the value of...
- 14M.2.sl.TZ2.6f: The water tank is shown below. It is partially filled with water. Find the value of \(x\)...
- 14M.2.sl.TZ2.6d: The water tank is shown below. It is partially filled with water. Calculate the value of y...
- 14M.1.sl.TZ1.13a: Write down the value of \(c\).
- 14M.1.sl.TZ1.13b: By using the coordinates of the vertex, B, or otherwise, write down two equations in \(a\)...
- 15M.1.sl.TZ1.14b: The vertex of the function is \((3,{\text{ }}27)\). Find the value of \(p\).
- 15M.1.sl.TZ1.14a: Calculate the value of \(q\).
- 15M.1.sl.TZ2.15c: When the width of the construction site is \(b\) metres, the site has a maximum area. (i) ...
- 15M.1.sl.TZ2.15d: The range of \(A(x)\) is \(m \leqslant A(x) \leqslant n\). Hence write down the value of...
- 15M.1.sl.TZ1.14c: The vertex of the function is \((3,{\text{ }}27)\). Write down the range of \(f\).
- 15M.1.sl.TZ2.15b: Site T has the same area as site S, but a different width. Find the width of T.
- 14N.1.sl.TZ0.14a: Draw the axis of symmetry on the following axes. The graph of the quadratic function...
- 14N.1.sl.TZ0.14b: The graph of the quadratic function intersects the \(x\)-axis at the point...
- 14N.1.sl.TZ0.14c: (i) Find the value of \(b\) and the value of \(c\). (ii) Draw the graph of the...
