| Date | May 2014 | Marks available | 1 | Reference code | 14M.2.sl.TZ2.6 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Hence | Question number | 6 | Adapted from | N/A |
Question
The front view of the edge of a water tank is drawn on a set of axes shown below.
The edge is modelled by \(y = a{x^2} + c\).
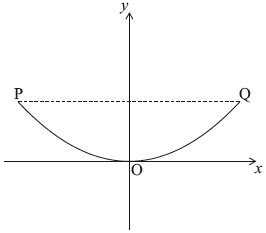
Point \({\text{P}}\) has coordinates \((-3, 1.8)\), point \({\text{O}}\) has coordinates \((0, 0)\) and point \({\text{Q}}\) has coordinates \((3, 1.8)\).
Write down the value of \(c\).
Find the value of \(a\).
Hence write down the equation of the quadratic function which models the edge of the water tank.
The water tank is shown below. It is partially filled with water.
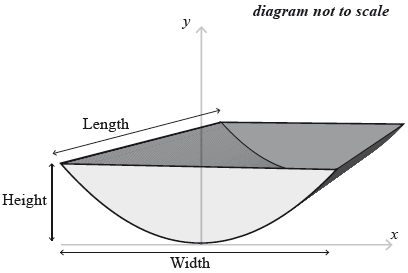
Calculate the value of y when \(x = 2.4{\text{ m}}\).
The water tank is shown below. It is partially filled with water.
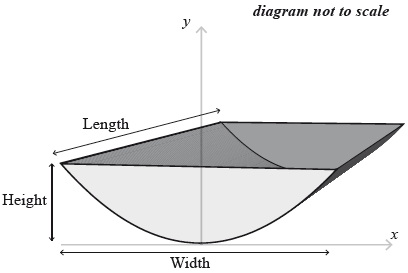
State what the value of \(x\) and the value of \(y\) represent for this water tank.
The water tank is shown below. It is partially filled with water.
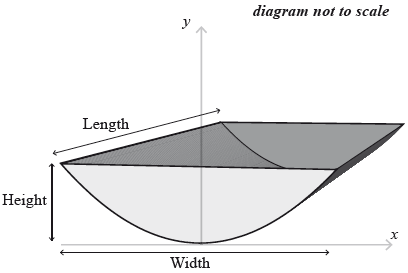
Find the value of \(x\) when the height of water in the tank is \(0.9\) m.
The water tank is shown below. It is partially filled with water.
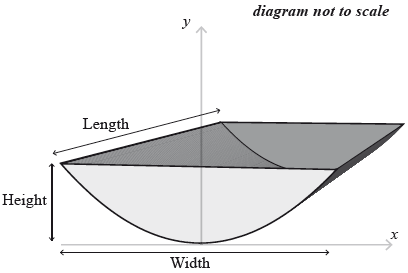
The water tank has a length of 5 m.
When the water tank is filled to a height of \(0.9\) m, the front cross-sectional area of the water is \({\text{2.55 }}{{\text{m}}^2}\).
(i) Calculate the volume of water in the tank.
The total volume of the tank is \({\text{36 }}{{\text{m}}^3}\).
(ii) Calculate the percentage of water in the tank.
Markscheme
\(0\) (A1)(G1)
[1 mark]
\(1.8 = a{(3)^2} + 0\) (M1)
OR
\(1.8 = a{( - 3)^2} + 0\) (M1)
Note: Award (M1) for substitution of \(y = 1.8\) or \(x = 3\) and their value of \(c\) into equation. \(0\) may be implied.
\(a = 0.2\) \(\left( {\frac{1}{5}} \right)\) (A1)(ft)(G1)
Note: Follow through from their answer to part (a).
Award (G1) for a correct answer only.
[2 marks]
\(y = 0.2{x^2}\) (A1)(ft)
Note: Follow through from their answers to parts (a) and (b).
Answer must be an equation.
[1 mark]
\(0.2 \times {(2.4)^2}\) (M1)
\( = 1.15{\text{ (m)}}\) \((1.152)\) (A1)(ft)(G1)
Notes: Award (M1) for correctly substituted formula, (A1) for correct answer. Follow through from their answer to part (c).
Award (G1) for a correct answer only.
[2 marks]
\(y\) is the height (A1)
positive value of \(x\) is half the width (or equivalent) (A1)
[2 marks]
\(0.9 = 0.2{x^2}\) (M1)
Note: Award (M1) for setting their equation equal to \(0.9\).
\(x = \pm 2.12{\text{ (m)}}\) \(\left( { \pm \frac{3}{2}\sqrt 2 ,{\text{ }} \pm \sqrt {4.5} ,{\text{ }} \pm {\text{2.12132}} \ldots } \right)\) (A1)(ft)(G1)
Note: Accept \(2.12\). Award (G1) for a correct answer only.
[2 marks]
(i) \(2.55 \times 5\) (M1)
Note: Award (M1) for correct substitution in formula.
\( = 12.8{\text{ (}}{{\text{m}}^3}{\text{)}}\) \(\left( {{\text{12.75 (}}{{\text{m}}^3}{\text{)}}} \right)\) (A1)(G2)
[2 marks]
(ii) \(\frac{{12.75}}{{36}} \times 100\) (M1)
Note: Award (M1) for correct quotient multiplied by \(100\).
\( = 35.4 (\%)\) \((35.4166 \ldots )\) (A1)(ft)(G2)
Note: Award (G2) for \(35.6 (\%) (35.5555… (\%))\).
Follow through from their answer to part (g)(i).
[2 marks]

