| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ2.12 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 12 | Adapted from | N/A |
Question
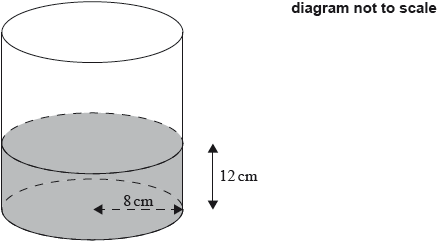
A cylindrical container with a radius of 8 cm is placed on a flat surface. The container is filled with water to a height of 12 cm, as shown in the following diagram.
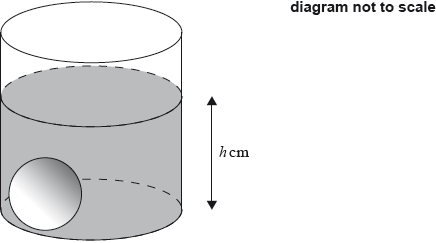
A heavy ball with a radius of 2.9 cm is dropped into the container. As a result, the height of the water increases to \(h\) cm, as shown in the following diagram.
Find the volume of water in the container.
Find the value of \(h\).
Markscheme
\(\pi \times {8^2} \times 12\) (M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula.
\(2410{\text{ c}}{{\text{m}}^3}{\text{ }}(2412.74 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}768\pi {\text{ c}}{{\text{m}}^3})\) (A1) (C2)
[2 marks]
\(\frac{4}{3}\pi \times {2.9^3} + 768\pi = \pi \times {8^2}h\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a sphere formula (this may be implied by seeing 102.160…), (M1) for adding their volume of the ball to their part (a), (M1) for equating a volume to the volume of a cylinder with a height of \(h\).
OR
\(\frac{4}{3}\pi \times {2.9^3} = \pi \times {8^2}(h - 12)\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a sphere formula (this may be implied by seeing 102.160…), (M1) for equating to the volume of a cylinder, (M1) for the height of the water level increase, \(h - 12\). Accept \(h\) for \(h - 12\) if adding 12 is implied by their answer.
\((h = ){\text{ }}12.5{\text{ (cm) }}\left( {12.5081 \ldots {\text{ (cm)}}} \right)\) (A1)(ft) (C4)
Note: If 3 sf answer used, answer is 12.5 (12.4944…). Follow through from part (a) if first method is used.
[4 marks]

