| Date | November 2016 | Marks available | 1 | Reference code | 16N.2.sl.TZ0.6 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Write down | Question number | 6 | Adapted from | N/A |
Question
A water container is made in the shape of a cylinder with internal height \(h\) cm and internal base radius \(r\) cm.
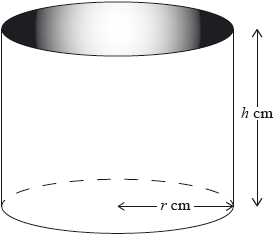
The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is \(0.5{\text{ }}{{\text{m}}^3}\).
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of \(2000{\text{ c}}{{\text{m}}^2}\).
Write down a formula for \(A\), the surface area to be coated.
Express this volume in \({\text{c}}{{\text{m}}^3}\).
Write down, in terms of \(r\) and \(h\), an equation for the volume of this water container.
Show that \(A = \pi {r^2}\frac{{1\,000\,000}}{r}\).
Show that \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\).
Find \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).
Using your answer to part (e), find the value of \(r\) which minimizes \(A\).
Find the value of this minimum area.
Find the least number of cans of water-resistant material that will coat the area in part (g).
Markscheme
\((A = ){\text{ }}\pi {r^2} + 2\pi rh\) (A1)(A1)
Note: Award (A1) for either \(\pi {r^2}\) OR \(2\pi rh\) seen. Award (A1) for two correct terms added together.
[2 marks]
\(500\,000\) (A1)
Notes: Units not required.
[1 mark]
\(500\,000 = \pi {r^2}h\) (A1)(ft)
Notes: Award (A1)(ft) for \(\pi {r^2}h\) equating to their part (b).
Do not accept unless \(V = \pi {r^2}h\) is explicitly defined as their part (b).
[1 mark]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).
[2 marks]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).
[2 marks]
\(2\pi r - \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\), (A1) for \(\frac{1}{{{r^2}}}\) or \({r^{ - 2}}\), (A1) for \( - {\text{1}}\,{\text{000}}\,{\text{000}}\).
[3 marks]
\(2\pi r - \frac{{1\,000\,000}}{{{r^2}}} = 0\) (M1)
Note: Award (M1) for equating their part (e) to zero.
\({r^3} = \frac{{1\,000\,000}}{{2\pi }}\) OR \(r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}\) (M1)
Note: Award (M1) for isolating \(r\).
OR
sketch of derivative function (M1)
with its zero indicated (M1)
\((r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )\) (A1)(ft)(G2)
[3 marks]
\(\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}\) (M1)
Note: Award (M1) for correct substitution of their part (f) into the given equation.
\( = 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )\) (A1)(ft)(G2)
[2 marks]
\(\frac{{27\,679.0 \ldots }}{{2000}}\) (M1)
Note: Award (M1) for dividing their part (g) by 2000.
\( = 13.8395 \ldots \) (A1)(ft)
Notes: Follow through from part (g).
14 (cans) (A1)(ft)(G3)
Notes: Final (A1) awarded for rounding up their \(13.8395 \ldots \) to the next integer.
[3 marks]

