| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
A type of candy is packaged in a right circular cone that has volume \({\text{100 c}}{{\text{m}}^{\text{3}}}\) and vertical height 8 cm.
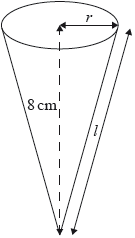
Find the radius, \(r\), of the circular base of the cone.
Find the slant height, \(l\), of the cone.
Find the curved surface area of the cone.
Markscheme
\(100 = \frac{1}{3}\pi {r^2}(8)\) (M1)
Note: Award (M1) for correct substitution into volume of cone formula.
\(r = 3.45{\text{ (cm) }}\left( {3.45494 \ldots {\text{ (cm)}}} \right)\) (A1) (C2)
[2 marks]
\({l^2} = {8^2} + {(3.45494 \ldots )^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ theorem.
\(l = 8.71{\text{ (cm) }}\left( {8.71416 \ldots {\text{ (cm)}}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (a).
[2 marks]
\(\pi \times 3.45494 \ldots \times 8.71416 \ldots \) (M1)
Note: Award (M1) for their correct substitutions into curved surface area of a cone formula.
\( = 94.6{\text{ c}}{{\text{m}}^2}{\text{ }}(94.5836 \ldots {\text{ c}}{{\text{m}}^2})\) (A1)(ft) (C2)
Note: Follow through from parts (a) and (b). Accept \(94.4{\text{ c}}{{\text{m}}^2}\) from use of 3 sf values.
[2 marks]

