| Date | November 2014 | Marks available | 1 | Reference code | 14N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 3 | Adapted from | N/A |
Question
Tepees were traditionally used by nomadic tribes who lived on the Great Plains of North America. They are cone-shaped dwellings and can be modelled as a cone, with vertex O, shown below. The cone has radius, \(r\), height, \(h\), and slant height, \(l\).
A model tepee is displayed at a Great Plains exhibition. The curved surface area of this tepee is covered by a piece of canvas that is \(39.27{\text{ }}{{\text{m}}^2}\), and has the shape of a semicircle, as shown in the following diagram.
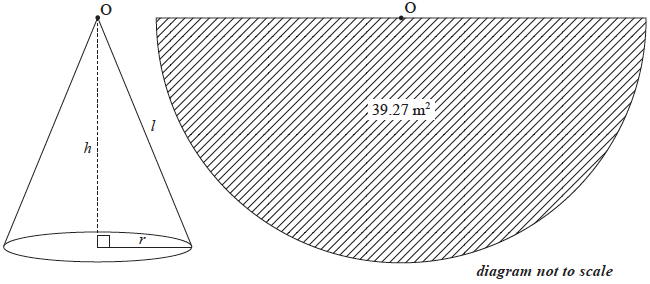
Show that the slant height, \(l\), is \(5\) m, correct to the nearest metre.
(i) Find the circumference of the base of the cone.
(ii) Find the radius, \(r\), of the base.
(iii) Find the height, \(h\).
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
Write down an expression for the height, \(h\), in terms of the radius, \(r\), of these cone-shaped tents.
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
Show that the volume of the tent, \(V\), can be written as
\[V = 3.11\pi {r^2} - \frac{2}{3}\pi {r^3}.\]
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
Find \(\frac{{{\text{d}}V}}{{{\text{d}}r}}\).
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
(i) Determine the exact value of \(r\) for which the volume is a maximum.
(ii) Find the maximum volume.
Markscheme
\(\frac{{\pi {l^2}}}{2} = 39.27\) (M1)(A1)
Note: Award (M1) for equating the formula for area of a semicircle to \(39.27\), award (A1) for correct substitution of \(l\) into the formula for area of a semicircle.
\(l = 5{\text{ (m)}}\) (AG)
(i) \(5 \times \pi \) (M1)
\( = 15.7\;\;\;(15.7079...,{\text{ }}5\pi )\;{\text{(m)}}\) (A1)(G2)
(ii) \(2\pi r = 15.7079…\;\;\;\)OR\(\;\;\;5\pi r = 39.27\) (M1)
\((r = ){\text{ 2.5 (m)}}\) (A1)(ft)(G2)
Note: Follow through from part (b)(i).
(iii) \(({h^2} = ){\text{ }}{5^2} - {2.5^2}\) (M1)
Notes: Award (M1) for correct substitution into Pythagoras’ theorem. Follow through from part (b)(ii).
\((h = ){\text{ 4.33 }}(4.33012 \ldots ){\text{ (m)}}\) (A1)(ft)(G2)
\(9.33 - 2 \times r\) (A1)
\(V = \frac{{\pi {r^2}}}{3} \times (9.33 - 2r)\) (M1)
Note: Award (M1) for correct substitution in the volume formula.
\(V = 3.11\pi {r^2} - \frac{2}{3}{\pi ^3}\) (AG)
\(6.22\pi r - 2\pi {r^2}\) (A1)(A1)
Notes: Award (A1) for \(6.22\pi r\), (A1) for \( - 2\pi {r^2}\).
If extra terms present, award at most (A1)(A0).
(i) \(6.22\pi r - 2\pi {r^2} = 0\) (M1)
Note: Award (M1) for setting their derivative from part (e) to 0.
\(r = 3.11{\text{ (m)}}\) (A1)(ft)(G2)
Notes: Award (A1) for identifying 3.11 as the answer.
Follow through from their answer to part (e).
(ii) \(\frac{1}{3}\pi {(3.11)^3}\;\;\;\)OR\(\;\;\;3.11\pi {(3.11)^2} - \frac{2}{3}\pi {(3.11)^3}\) (M1)
Note: Award (M1) for correct substitution into the correct volume formula.
\(31.5{\text{ (}}{{\text{m}}^3}{\text{)}}{\text{(31.4999}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from their answer to part (f)(i).

