| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Calculate | Question number | 9 | Adapted from | N/A |
Question
A right pyramid has apex \({\text{V}}\) and rectangular base \({\text{ABCD}}\), with \({\text{AB}} = 8{\text{ cm}}\), \({\text{BC}} = 6{\text{ cm}}\) and \({\text{VA}} = 13{\text{ cm}}\). The vertical height of the pyramid is \({\text{VM}}\).
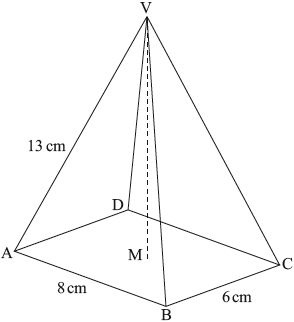
Calculate \({\text{VM}}\).
Calculate the volume of the pyramid.
Markscheme
\({\text{A}}{{\text{C}}^2} = {8^2} + {6^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras, or recognition of Pythagorean triple.
\({\text{AC}} = 10\) (A1)
Note: Award (A2) for \({\text{AC}} = 10\;\;\;\)OR\(\;\;\;{\text{AM}} = 5\) with no working seen.
\({\text{V}}{{\text{M}}^2} = {13^2} - {5^2}\) (M1)
Note: Award (M1) for correct second use of Pythagoras, using the result from the first use of Pythagoras.
\({\text{VM}} = 12{\text{ (cm)}}\) (A1) (C4)
Notes: Accept alternative methods and apply the markscheme as follows: Award (M1)(A1) for first correct use of Pythagoras with lengths from the question, (M1) for a correct second use of Pythagoras, consistent with the method chosen, (A1) for correct height.
\(\frac{1}{3} \times 8 \times 6{\kern 1pt} \times 12\) (M1)
Note: Award (M1) for their correct substitutions into volume formula.
\( = 192{\text{ c}}{{\text{m}}^3}\) (A1)(ft) (C2)
Notes: Follow through from part (a), only if working seen.
Examiners report
In part (a) many candidates struggled to identify right angled triangles correctly. A regular mistake was to calculate the slant height and not the vertical height. Often values were used which did not correspond to a right angled triangle in the diagram, such as 13 and 8. Another common mistake was incorrect use of Pythagoras, where the hypotenuse was not correctly identified or was incorrectly substituted into the formula.
Despite the problems to obtain a correct answer for part (a), in part (b) many candidates wrote down a correctly substituted formula for the volume of a pyramid (with their height substituted) and received follow through marks. Very few, having calculated their volume correctly, failed to give the correct units. Some candidates used the perimeter (28) of the base and not the area.

