| Date | May 2014 | Marks available | 4 | Reference code | 14M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Calculate | Question number | 8 | Adapted from | N/A |
Question
A child’s wooden toy consists of a hemisphere, of radius 9 cm , attached to a cone with the same base radius. O is the centre of the base of the cone and V is vertically above O.
Angle OVB is \({27.9^ \circ }\).
Diagram not to scale.
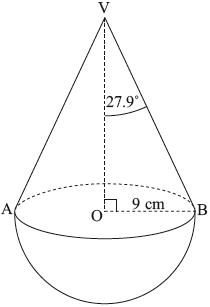
Calculate OV, the height of the cone.
Calculate the volume of wood used to make the toy.
Markscheme
\(\tan 27.9^\circ = \frac{9}{{{\text{OV}}}}\) (M1)
Note: Award (M1) for correct substitution in trig formula.
\({\text{OV}} = 17.0\left( {{\text{cm}}} \right)\left( {16.9980 \ldots } \right)\) (A1) (C2)
[2 marks]
\(\frac{{\pi {{(9)}^2}(16.9980 \ldots )}}{3} + \frac{1}{2} \times \frac{{4\pi {{(9)}^3}}}{3}\) (M1)(M1)(M1)
Note: Award (M1) for correctly substituted volume of the cone, (M1) for correctly substituted volume of a sphere divided by two (hemisphere), (M1) for adding the correctly substituted volume of the cone to either a correctly substituted sphere or hemisphere.
\( = 2970{\text{ c}}{{\text{m}}^3}{\text{ (2968.63}} \ldots {\text{)}}\) (A1)(ft) (C4)
Note: The answer is \(2970{\text{ c}}{{\text{m}}^3}\), the units are required.
[4 marks]

