| Date | November 2012 | Marks available | 3 | Reference code | 12N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
A contractor is building a house. He first marks out three points A , B and C on the ground such that AB = 5 m , AC = 7 m and angle BAC = 112 °.
Find the length of BC.
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
Find the size of angle DBC .
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
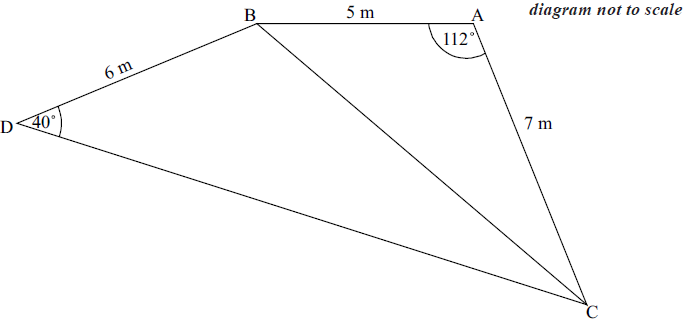
Find the area of the quadrilateral ABDC.
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
The contractor digs up and removes the soil under the quadrilateral ABDC to a depth of 50 cm for the foundation of the house.
Find the volume of the soil removed. Give your answer in m3 .
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
The contractor digs up and removes the soil under the quadrilateral ABDC to a depth of 50 cm for the foundation of the house.
To transport the soil removed, the contractor uses cylindrical drums with a diameter of 30 cm and a height of 40 cm.
(i) Find the volume of a drum. Give your answer in m3 .
(ii) Find the minimum number of drums required to transport the soil removed.
Markscheme
Units are required in part (c) only.
BC2 = 52 + 72 − 2(5)(7)cos112° (M1)(A1)
Note: Award (M1) for substitution in cosine formula, (A1) for correct substitutions.
BC = 10.0 (m) (10.0111...) (A1)(G2)
Note: If radians are used, award at most (M1)(A1)(A0).
[3 marks]
Units are required in part (c) only.
\(\frac{{\sin 40^\circ }}{{10.0111...}} = \frac{{\sin {\text{D}}{\operatorname{\hat C}}{\text{B}}}}{6}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution in sine formula, (A1)(ft) for their correct substitutions. Follow through from their part (a).
\({\text{D}}{\operatorname {\hat C}}{\text{B}}\) = 22.7° (22.6589...) (A1)(ft)
Notes: Award (A2) for 22.7° seen without working. Use of radians results in unrealistic answer. Award a maximum of (M1)(A1)(ft)(A0)(ft). Follow through from their part (a).
\({\text{D}}{\operatorname {\hat C}}{\text{B}}\) = 117° (117.341...) (A1)(ft)(G3)
Notes: Do not penalize if use of radians was already penalized in part (a). Follow through from their answer to part (a).
OR
From use of cosine formula
DC = 13.8(m) (13.8346…) (A1)(ft)
Note: Follow through from their answer to part (a).
\(\frac{{\sin \alpha }}{{13.8346...}} = \frac{{\sin 40^\circ }}{{10.0111...}}\) (M1)
Note: Award (M1) for correct substitution in the correct sine formula.
α = 62.7° (62.6589) (A1)(ft)
Note: Accept 62.5° from use of 3sf.
\({\text{D}}{\operatorname {\hat B}}{\text{C}}\) = 117(117.341...) (A1)(ft)
Note: Follow through from their part (a). Use of radians results in unrealistic answer, award a maximum of (A1)(M1)(A0)(A0).
[4 marks]
Units are required in part (c) only.
\({\text{ABDC}} = \frac{1}{2}(5)(7)\sin 112^\circ + \frac{1}{2}(6)(10.0111...)\sin 117.341...^\circ \) (M1)(A1)(ft)(M1)N
Note: Award (M1) for substitution in both triangle area formulae, (A1)(ft) for their correct substitutions, (M1) for seen or implied addition of their two triangle areas. Follow through from their answer to part (a) and (b).
= 42.9 m2 (42.9039...) (A1)(ft)(G3)
Notes: Answer is 42.9 m2 i.e. the units are required for the final (A1)(ft) to be awarded. Accept 43.0 m2 from using 3sf answers to parts (a) and (b). Do not penalize if use of radians was previously penalized.
[4 marks]
Units are required in part (c) only.
42.9039... × 0.5 (M1)(M1)
Note: Award (M1) for 0.5 seen (or equivalent), (M1) for multiplication of their answer in part (c) with their value for depth.
= 21.5 (m3) (21.4519...) (A1)(ft)(G3)
Note: Follow through from their part (c) only if working is seen. Do not penalize if use of radians was previously penalized. Award at most (A0)(M1)(A0)(ft) for multiplying by 50.
[3 marks]
Units are required in part (c) only.
(i) π(0.15)2(0.4) (M1)(A1)
OR
π × 152 × 40 (28274.3...) (M1)(A1)
Notes: Award (M1) for substitution in the correct volume formula. (A1) for correct substitutions.
= 0.0283 (m3) (0.0282743..., 0.09π)
(ii) \(\frac{{21.4519...}}{{0.0282743...}}\) (M1)
Note: Award (M1) for correct division of their volumes.
= 759 (A1)(ft)(G2)
Notes: Follow through from their parts (d) and (e)(i). Accept 760 from use of 3sf answers. Answer must be a positive integer for the final (A1)(ft) mark to be awarded.
[5 marks]
Examiners report
The responses to this question showed appropriate use of sine and cosine formulae for the most part. A few students still used the Pythagorean formula incorrectly, although the given triangles were not right ones. There was an occasional use of GDC set to radians, and very few students lost marks for giving their answers in radians. In part (d), converting from cm3 to m3 was largely problematic for the great majority of students. Part (e) also was difficult for some students, as it requires some interpretation before the volume formula is used.
The responses to this question showed appropriate use of sine and cosine formulae for the most part. A few students still used the Pythagorean formula incorrectly, although the given triangles were not right ones. There was an occasional use of GDC set to radians, and very few students lost marks for giving their answers in radians. In part (d), converting from cm3 to m3 was largely problematic for the great majority of students. Part (e) also was difficult for some students, as it requires some interpretation before the volume formula is used.
The responses to this question showed appropriate use of sine and cosine formulae for the most part. A few students still used the Pythagorean formula incorrectly, although the given triangles were not right ones. There was an occasional use of GDC set to radians, and very few students lost marks for giving their answers in radians. In part (d), converting from cm3 to m3 was largely problematic for the great majority of students. Part (e) also was difficult for some students, as it requires some interpretation before the volume formula is used.
The responses to this question showed appropriate use of sine and cosine formulae for the most part. A few students still used the Pythagorean formula incorrectly, although the given triangles were not right ones. There was an occasional use of GDC set to radians, and very few students lost marks for giving their answers in radians. In part (d), converting from cm3 to m3 was largely problematic for the great majority of students. Part (e) also was difficult for some students, as it requires some interpretation before the volume formula is used.
The responses to this question showed appropriate use of sine and cosine formulae for the most part. A few students still used the Pythagorean formula incorrectly, although the given triangles were not right ones. There was an occasional use of GDC set to radians, and very few students lost marks for giving their answers in radians. In part (d), converting from cm3 to m3 was largely problematic for the great majority of students. Part (e) also was difficult for some students, as it requires some interpretation before the volume formula is used.

