| Date | May 2017 | Marks available | 1 | Reference code | 17M.1.sl.TZ2.11 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 11 | Adapted from | N/A |
Question
The mass of a certain type of Chilean corncob follows a normal distribution with a mean of 400 grams and a standard deviation of 50 grams.
A farmer labels one of these corncobs as premium if its mass is greater than \(a\) grams. 25% of these corncobs are labelled as premium.
Write down the probability that the mass of one of these corncobs is greater than 400 grams.
Find the value of \(a\).
Estimate the interquartile range of the distribution.
Markscheme
\(0.5{\text{ }}\left( {50\% ,{\text{ }}\frac{1}{2}} \right)\) (A1) (C1)
[1 mark]
\({\text{P}}(X > a) = 0.25\)\(\,\,\,\)OR\(\,\,\,\)\({\text{P}}(X < a) = 0.75\) (M1)
Note: Award (M1) for a sketch of approximate normal curve with a vertical line drawn to the right of the mean with the area to the right of this line shaded.
\(a = 434{\text{ (g) }}\left( {433.724 \ldots {\text{ (g)}}} \right)\) (A1) (C2)
[2 marks]
\(33.7244 \ldots \times 2\) (A1)(ft)(M1)
Note: Award (A1)(ft) for \(33.7244 \ldots {\text{ }}({\text{or }}433.7244 \ldots {\text{ }} - {\text{ }}400)\) seen, award (M1) for multiplying their 33.7244… by 2. Follow through from their answer to part (b).
OR
\(434 - 366.275 \ldots \) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \(366.275 \ldots {\text{ }}(366)\) seen, (M1) for difference between their answer to (b) and their 366.
OR
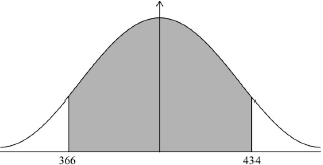 (A1)(ft)(M1)
(A1)(ft)(M1)
Note: Award (A1)(ft) for their \(366.275 \ldots {\text{ }}(366)\) seen. Award (M1) for correct symmetrical region indicated on labelled normal curve.
67.4 (g) (A1)(ft) (C3)
Note: Accept an answer of 68 from use of rounded values. Follow through from part (b).
[3 marks]

