| Date | May 2014 | Marks available | 2 | Reference code | 14M.1.sl.TZ2.14 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 14 | Adapted from | N/A |
Question
The heights of apple trees in an orchard are normally distributed with a mean of \({\text{3.42 m}}\) and a standard deviation of \({\text{0.21 m}}\).
Write down the probability that a randomly chosen tree has a height greater than \({\text{3.42 m}}\).
Write down the probability that a randomly chosen tree will be within 2 standard deviations of the mean of \({\text{3.42 m}}\).
Use your graphic display calculator to calculate the probability that a randomly chosen tree will have a height greater than \({\text{3.35 m}}\).
The probability that a particular tree is less than \(x\) metres high is \(0.65\). Find the value of \(x\).
Markscheme
\(0.5{\text{ }}\left( {50\% ,{\text{ }}\frac{{50}}{{100}},{\text{ }}\frac{1}{2}} \right)\) (A1) (C1)
[1 mark]
\(0.954 (0.954499…, 95.4\%, 95.4499…\%)\) (A1) (C1)
Note: Accept \(95\%\) or \(0.95\).
[1 mark]
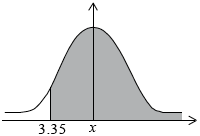 (M1)
(M1)
Note: Accept alternative methods.
\(0.631 (0.630558…, 63.1\%, 63.0558…\%)\) (A1) (C2)
[2 marks]
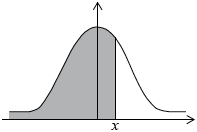 (M1)
(M1)
Note: Accept alternative methods.
\(3.50{\text{ }} (3.50091...)\) (A1) (C2)
[2 marks]

