| Date | November 2017 | Marks available | 2 | Reference code | 17N.1.sl.TZ0.13 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Estimate | Question number | 13 | Adapted from | N/A |
Question
Applicants for a job had to complete a mathematics test. The time they took to complete the test is normally distributed with a mean of 53 minutes and a standard deviation of 16.3. One of the applicants is chosen at random.
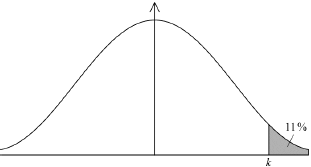
For 11% of the applicants it took longer than \(k\) minutes to complete the test.
There were 400 applicants for the job.
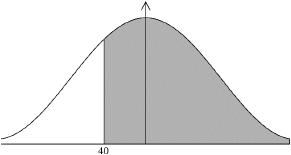
Find the probability that this applicant took at least 40 minutes to complete the test.
Find the value of \(k\).
Estimate the number of applicants who completed the test in less than 25 minutes.
Markscheme
0.787 (0.787433…, 78.7%) (M1)(A1) (C2)
Note: Award (M1) for a correct probability statement, \({\text{P}}(X > 40)\), or a correctly shaded normal distribution graph.
[2 marks]
73.0 (minutes) (72.9924…) (M1)(A1) (C2)
Note: Award (M1) for a correct probability statement, \({\text{P}}(X > k) = 0.11\), or a correctly shaded normal distribution graph.
[2 marks]
\(0.0423433 \ldots \times 400\) (M1)
Note: Award (M1) for multiplying a probability by 400. Do not award (M1) for \(0.11 \times 400\).
Use of a lower bound less than zero gives a probability of 0.0429172….
\( = 16\) (A1) (C2)
Notes: Accept a final answer of 17. Do not accept a final answer of 18. Accept a non-integer final answer either 16.9 (16.9373…) from use of lower bound zero or 17.2 (17.1669…) from use of the default lower bound of \(-{10^{99}}\).
[2 marks]

