| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ2.13 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Shade | Question number | 13 | Adapted from | N/A |
Question
A factory makes metal bars. Their lengths are assumed to be normally distributed with a mean of 180 cm and a standard deviation of 5 cm.
On the following diagram, shade the region representing the probability that a metal bar, chosen at random, will have a length less than 175 cm.
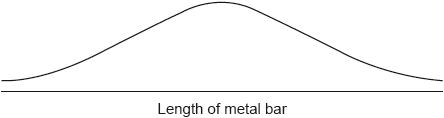
A metal bar is chosen at random.
(i) The probability that the length of the metal bar is less than 175 cm is equal to the probability that the length is greater than \(h\) cm. Write down the value of \(h\).
(ii) Find the probability that the length of the metal bar is greater than one standard deviation above the mean.
Markscheme
(A1)(M1) (C2)
Notes: Award (A1) for the vertical line labelled as \(175{\text{ (cm)}}\).
Award (M1) for a vertical line drawn to the left of the mean with the area to the left of this line shaded.
Accept \(( - )1\) sd marked on the diagram for \(175\) (provided line is to the left of the mean).
(i) \(185{\text{ (cm)}}\) (A1)(C1)
(ii) \({\text{P(length}} > 185)\) (A1)(M1)
Note: Award (A1) for the vertical line labelled as \(185{\text{ (cm)}}\).
Award (M1) for a vertical line drawn to the right of the mean with the area to the right of this line shaded.
Accept 1 sd marked on the diagram for \(185\) (provided line is to the right of the mean).
\( = 0.159\;\;\;(0.158655 \ldots )\) (A1) (C3)

