| Date | November 2016 | Marks available | 2 | Reference code | 16N.2.sl.TZ0.4 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Calculate | Question number | 4 | Adapted from | N/A |
Question
A manufacturer produces 1500 boxes of breakfast cereal every day.
The weights of these boxes are normally distributed with a mean of 502 grams and a standard deviation of 2 grams.
All boxes of cereal with a weight between 497.5 grams and 505 grams are sold. The manufacturer’s income from the sale of each box of cereal is $2.00.
The manufacturer recycles any box of cereal with a weight not between 497.5 grams and 505 grams. The manufacturer’s recycling cost is $0.16 per box.
A different manufacturer produces boxes of cereal with weights that are normally distributed with a mean of 350 grams and a standard deviation of 1.8 grams.
This manufacturer sells all boxes of cereal that are above a minimum weight, \(w\).
They sell 97% of the cereal boxes produced.
Draw a diagram that shows this information.
(i) Find the probability that a box of cereal, chosen at random, is sold.
(ii) Calculate the manufacturer’s expected daily income from these sales.
Calculate the manufacturer’s expected daily recycling cost.
Calculate the value of \(w\).
Markscheme
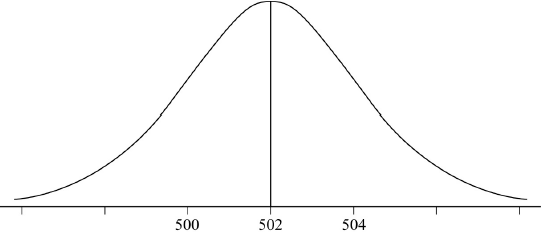
(A1)(A1)
Notes: Award (A1) for bell shape with mean of 502.
Award (A1) for an indication of standard deviation eg 500 and 504.
[2 marks]
(i) \(0.921{\text{ }}(0.920968 \ldots ,{\text{ }}92.0968 \ldots \% )\) (G2)
Note: Award (M1) for a diagram showing the correct shaded region.
(ii) \(1500 \times 2 \times 0.920968 \ldots \) (M1)
\( = {\text{ }}(\$ ){\text{ }}2760{\text{ }}(2762.90 \ldots )\) (A1)(ft)(G2)
Note: Follow through from their answer to part (b)(i).
[4 marks]
\(1500 \times 0.16 \times 0.079031 \ldots \) (M1)
Notes: Award (A1) for \(1500 \times 0.16 \times {\text{ their }}(1 - 0.920968 \ldots )\).
OR
\((1500 - 1381.45) \times 0.16\) (M1)
Notes: Award (M1) for \((1500 - {\text{their }}1381.45) \times 0.16\).
\( = (\$ )19.0{\text{ (}}18.9676 \ldots )\) (A1)(ft)(G2)
[2 marks]
\(347{\text{ }}({\text{grams}}){\text{ }}(346.614 \ldots )\) (G3)
Notes: Award (G2) for an answer that rounds to 346.
Award (G1) for \(353.385 \ldots \) seen without working (for finding the top 3%).
[3 marks]

