| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.sl.TZ1.5 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Determine | Question number | 5 | Adapted from | N/A |
Question
A group of candidates sat a Chemistry examination and a Physics examination. The candidates’ marks in the Chemistry examination are normally distributed with a mean of \(60\) and a standard deviation of \(12\).
Draw a diagram that shows this information.
Write down the probability that a randomly chosen candidate who sat the Chemistry examination scored at most 60 marks.
Hee Jin scored 80 marks in the Chemistry examination.
Find the probability that a randomly chosen candidate who sat the Chemistry examination scored more than Hee Jin.
The candidates’ marks in the Physics examination are normally distributed with a mean of \(63\) and a standard deviation of \(10\). Hee Jin also scored \(80\) marks in the Physics examination.
Find the probability that a randomly chosen candidate who sat the Physics examination scored less than Hee Jin.
The candidates’ marks in the Physics examination are normally distributed with a mean of \(63\) and a standard deviation of \(10\). Hee Jin also scored \(80\) marks in the Physics examination.
Determine whether Hee Jin’s Physics mark, compared to the other candidates, is better than her mark in Chemistry. Give a reason for your answer.
To obtain a “grade A” a candidate must be in the top \(10\% \) of the candidates who sat the Physics examination.
Find the minimum possible mark to obtain a “grade A”. Give your answer correct to the nearest integer.
Markscheme
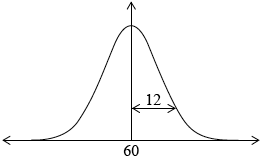(A1)(A1)
Notes: Award (A1) for rough sketch of normal curve centred at \(60\), (A1) for some indication of \(12\) as the standard deviation eg, as diagram, or with \(72\) and \(48\) shown on the horizontal axis in appropriate places, or for \(96\) and \(24\) shown on the horizontal axis in appropriate places.
[2 marks]
\(0.5 \left( {\frac{1}{2},{\text{ 50% }}} \right)\) (A1)
Note: Accept only the exact answer.
[1 mark]
\(0.0478{\text{ }} (0.0477903...)\) (G2)
Note: Award (G1) for \(0.952209…\), award (M1)(G0) for diagram with correct area shown but incorrect answer.
[2 marks]
\(0.955 {\text{ }} (0.955434...)\) (G2)
Note: Award (G1) for \(0.044565…\), award (M1)(G0) for diagram with correct area shown but incorrect answer.
[2 marks]
\(0.0446 < 0.0478\) (R1)
Notes: Award (R1) for correct comparison seen. Accept alternative methods, for example, \(1–\) (their answer to part (c)) used in comparison or a comparison based on \(z\) scores.
the Physics result is better (A1)(ft)
Notes: Do not award (R0)(A1). Follow through from their answers to part (c) and part (d).
[2 marks]
\(76\) (G3)
Notes: Award (G1) for \(75.8155…\), award (G2) for \(75\).
Award (M1)(G0) for diagram with correct area shown but incorrect answer.
[3 marks]
