| Date | May 2015 | Marks available | 1 | Reference code | 15M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f'\), the derivative of \(f\).
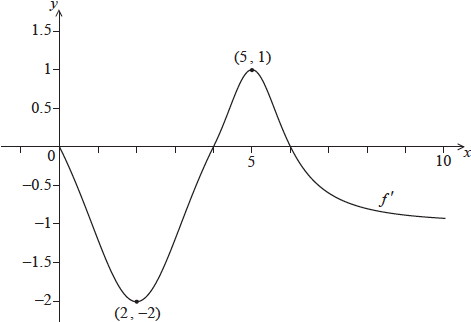
The graph of \(f'\) passes through \((2,{\text{ }} - 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g'\), the derivative of \(g\).
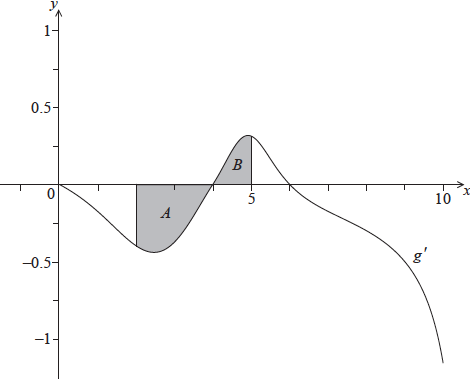
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f'\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = - 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)' \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g'\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( - 0.666667\)
\(g'(2) = - \frac{2}{3}{\text{ (exact), }} - 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) - g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) - g(2),{\text{ }}\ln 3 + g(a) - \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) - \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 - 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( - 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 - 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = - 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = - 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) - g(4) = 0.21,{\text{ }}g(2) - g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) - [\ln 3 - 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 - 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = - 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = - 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) - g(2) = - 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) - \ln 3 = - 0.45\)
\(0.648612\)
\(g(5) = \ln 3 - 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
Examiners report
In part (a), many candidates did not get full marks in justifying that \(p = 6\) was where the maximum occurs. The derivative changing from positive to negative was not sufficient since there are cases where the derivative changes signs at a value where there is no turning point. Part (c) was very poorly done as most candidates did not recognize the use of the chain rule to find the derivative of \(\ln \left( {f(x)} \right)\), a fairly basic application for Mathematics SL. In part (d), candidates appeared to have difficulty with the command term “verify”, and even if they were successful, did not make the connection to part (e) where they attempted a variety of interesting ways to find \(g(5)\) - the most common approach was to set up two incorrect integrals involving areas \(A\) and \(B\). Many students did not realize that integrating a function over an interval where the function is negative gives the opposite of the area between the function and the x-axis.
In part (a), many candidates did not get full marks in justifying that \(p = 6\) was where the maximum occurs. The derivative changing from positive to negative was not sufficient since there are cases where the derivative changes signs at a value where there is no turning point. Part (c) was very poorly done as most candidates did not recognize the use of the chain rule to find the derivative of \(\ln \left( {f(x)} \right)\), a fairly basic application for Mathematics SL. In part (d), candidates appeared to have difficulty with the command term “verify”, and even if they were successful, did not make the connection to part (e) where they attempted a variety of interesting ways to find \(g(5)\) - the most common approach was to set up two incorrect integrals involving areas A and B. Many students did not realize that integrating a function over an interval where the function is negative gives the opposite of the area between the function and the x-axis.
In part (a), many candidates did not get full marks in justifying that \(p = 6\) was where the maximum occurs. The derivative changing from positive to negative was not sufficient since there are cases where the derivative changes signs at a value where there is no turning point. Part (c) was very poorly done as most candidates did not recognize the use of the chain rule to find the derivative of \(\ln \left( {f(x)} \right)\), a fairly basic application for Mathematics SL. In part (d), candidates appeared to have difficulty with the command term “verify”, and even if they were successful, did not make the connection to part (e) where they attempted a variety of interesting ways to find \(g(5)\) - the most common approach was to set up two incorrect integrals involving areas A and B. Many students did not realize that integrating a function over an interval where the function is negative gives the opposite of the area between the function and the x-axis.
In part (a), many candidates did not get full marks in justifying that \(p = 6\) was where the maximum occurs. The derivative changing from positive to negative was not sufficient since there are cases where the derivative changes signs at a value where there is no turning point. Part (c) was very poorly done as most candidates did not recognize the use of the chain rule to find the derivative of \(\ln \left( {f(x)} \right)\), a fairly basic application for Mathematics SL. In part (d), candidates appeared to have difficulty with the command term “verify”, and even if they were successful, did not make the connection to part (e) where they attempted a variety of interesting ways to find \(g(5)\) - the most common approach was to set up two incorrect integrals involving areas A and B. Many students did not realize that integrating a function over an interval where the function is negative gives the opposite of the area between the function and the x-axis.
In part (a), many candidates did not get full marks in justifying that \(p = 6\) was where the maximum occurs. The derivative changing from positive to negative was not sufficient since there are cases where the derivative changes signs at a value where there is no turning point. Part (c) was very poorly done as most candidates did not recognize the use of the chain rule to find the derivative of \(\ln \left( {f(x)} \right)\), a fairly basic application for Mathematics SL. In part (d), candidates appeared to have difficulty with the command term “verify”, and even if they were successful, did not make the connection to part (e) where they attempted a variety of interesting ways to find \(g(5)\) - the most common approach was to set up two incorrect integrals involving areas A and B. Many students did not realize that integrating a function over an interval where the function is negative gives the opposite of the area between the function and the x-axis.

