| Date | November 2009 | Marks available | 1 | Reference code | 09N.1.sl.TZ0.9 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Describe | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = 3 + \frac{{20}}{{{x^2} - 4}}\) , for \(x \ne \pm 2\) . The graph of f is given below.
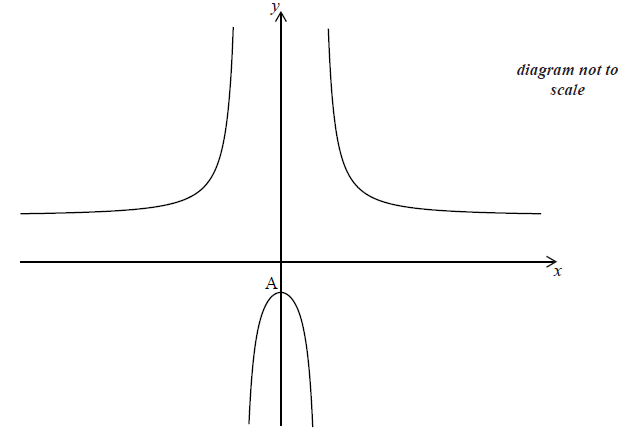
The y-intercept is at the point A.
(i) Find the coordinates of A.
(ii) Show that \(f'(x) = 0\) at A.
The second derivative \(f''(x) = \frac{{40(3{x^2} + 4)}}{{{{({x^2} - 4)}^3}}}\) . Use this to
(i) justify that the graph of f has a local maximum at A;
(ii) explain why the graph of f does not have a point of inflexion.
Describe the behaviour of the graph of \(f\) for large \(|x|\) .
Write down the range of \(f\) .
Markscheme
(i) coordinates of A are \((0{\text{, }} - 2)\) A1A1 N2
(ii) derivative of \({x^2} - 4 = 2x\) (seen anywhere) (A1)
evidence of correct approach (M1)
e.g. quotient rule, chain rule
finding \(f'(x)\) A2
e.g. \(f'(x) = 20 \times ( - 1) \times {({x^2} - 4)^{ - 2}} \times (2x)\) , \(\frac{{({x^2} - 4)(0) - (20)(2x)}}{{{{({x^2} - 4)}^2}}}\)
substituting \(x = 0\) into \(f'(x)\) (do not accept solving \(f'(x) = 0\) ) M1
at A \(f'(x) = 0\) AG N0
[7 marks]
(i) reference to \(f'(x) = 0\) (seen anywhere) (R1)
reference to \(f''(0)\) is negative (seen anywhere) R1
evidence of substituting \(x = 0\) into \(f''(x)\) M1
finding \(f''(0) = \frac{{40 \times 4}}{{{{( - 4)}^3}}}\) \(\left( { = - \frac{5}{2}} \right)\) A1
then the graph must have a local maximum AG
(ii) reference to \(f''(x) = 0\) at point of inflexion (R1)
recognizing that the second derivative is never 0 A1 N2
e.g. \(40(3{x^2} + 4) \ne 0\) , \(3{x^2} + 4 \ne 0\) , \({x^2} \ne - \frac{4}{3}\) , the numerator is always positive
Note: Do not accept the use of the first derivative in part (b).
[6 marks]
correct (informal) statement, including reference to approaching \(y = 3\) A1 N1
e.g. getting closer to the line \(y = 3\) , horizontal asymptote at \(y = 3\)
[1 mark]
correct inequalities, \(y \le - 2\) , \(y > 3\) , FT from (a)(i) and (c) A1A1 N2
[2 marks]
Examiners report
Almost all candidates earned the first two marks in part (a) (i), although fewer were able to apply the quotient rule correctly.
Many candidates were able to state how the second derivative can be used to identify maximum and inflection points, but fewer were actually able to demonstrate this with the given function. For example, in (b)(ii) candidates often simply said "the second derivative cannot equal 0" but did not justify or explain why this was true.
Not too many candidates could do part (c) correctly.
In (d) even those who knew what the range was had difficulty expressing the inequalities correctly.

