| Date | May 2010 | Marks available | 2 | Reference code | 10M.1.sl.TZ2.7 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Explain | Question number | 7 | Adapted from | N/A |
Question
A function f is defined for \( - 4 \le x \le 3\) . The graph of f is given below.
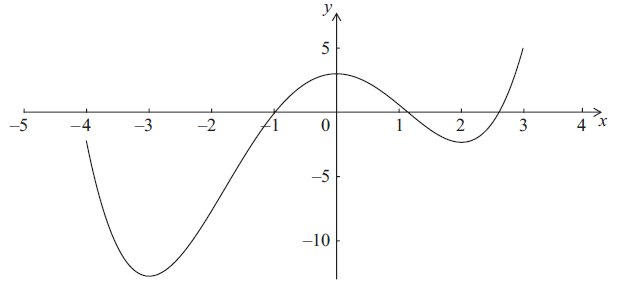
The graph has a local maximum when \(x = 0\) , and local minima when \(x = - 3\) , \(x = 2\) .
Write down the x-intercepts of the graph of the derivative function, \(f'\) .
Write down all values of x for which \(f'(x)\) is positive.
At point D on the graph of f , the x-coordinate is \( - 0.5\). Explain why \(f''(x) < 0\) at D.
Markscheme
x-intercepts at \( - 3\), 0, 2 A2 N2
[2 marks]
\( - 3 < x < 0\) , \(2 < x < 3\) A1A1 N2
[2 marks]
correct reasoning R2
e.g. the graph of f is concave-down (accept convex), the first derivative is decreasing
therefore the second derivative is negative AG
[2 marks]
Examiners report
Candidates had mixed success with parts (a) and (b). Weaker candidates either incorrectly used the x-intercepts of f or left this question blank. Some wrote down only two of the three values in part (a). Candidates who answered part (a) correctly often had trouble writing the set of values in part (b); difficulties included poor notation and incorrectly including the endpoints. Other candidates listed individual x-values here rather than a range of values.
Candidates had mixed success with parts (a) and (b). Weaker candidates either incorrectly used the x-intercepts of f or left this question blank. Some wrote down only two of the three values in part (a). Candidates who answered part (a) correctly often had trouble writing the set of values in part (b); difficulties included poor notation and incorrectly including the endpoints. Other candidates listed individual x-values here rather than a range of values.
Many candidates had difficulty explaining why the second derivative is negative in part (c). A number claimed that since the point D was “close” to a maximum value, the second derivative must be negative; this incorrect appeal to the second derivative test indicates a lack of understanding of how the test works and the relative concept of closeness. Some candidates claimed D was a point of inflexion, again demonstrating poor understanding of the second derivative. Among candidates who answered part (c) correctly, some stated that f was concave down while others gave well-formed arguments for why the first derivative was decreasing. A few candidates provided nicely sketched graphs of \(f'\) and \(f''\) and used them in their explanations.

