| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.4 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The following diagram shows the graph of a function \(f\).
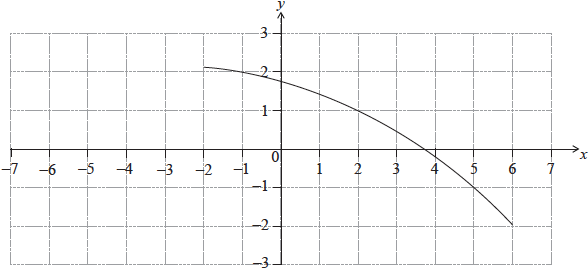
Find \({f^{ - 1}}( - 1)\).
Find \((f \circ f)( - 1)\).
On the same diagram, sketch the graph of \(y = f( - x)\).
Markscheme
valid approach (M1)
eg\(\;\;\;\)horizontal line on graph at \( - 1,{\text{ }}f(a) = - 1,{\text{ }}( - 1,5)\)
\({f^{ - 1}}( - 1) = 5\) A1 N2
[2 marks]
attempt to find \(f( - 1)\) (M1)
eg\(\;\;\;\)line on graph
\(f( - 1) = 2\) (A1)
\((f \circ f)( - 1) = 1\) A1 N3
[3 marks]
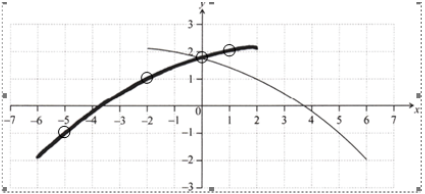 A1A1 N2
A1A1 N2
Note: The shape must be an approximately correct shape (concave down and increasing). Only if the shape is approximately correct, award the following for points in circles:
A1 for the \(y\)-intercept,
A1 for any two of these points \(( - 5,{\text{ }} - 1),{\text{ }}( - 2,{\text{ }}1),{\text{ }}(1,{\text{ }}2)\).
[2 marks]
Total [7 marks]
Examiners report
Typically candidates were more successful in finding the composite function than the inverse. Some students tried to find the function, rather than read values from the given graph. The sketch of \(f( - x)\) was often well done, with the most common error being a reflection in the x-axis.
Typically candidates were more successful in finding the composite function than the inverse. Some students tried to find the function, rather than read values from the given graph. The sketch of \(f( - x)\) was often well done, with the most common error being a reflection in the x-axis.
Typically candidates were more successful in finding the composite function than the inverse. Some students tried to find the function, rather than read values from the given graph. The sketch of \(f( - x)\) was often well done, with the most common error being a reflection in the x-axis.

