IB Questionbank

Loading [MathJax]/jax/output/CommonHTML/fonts/TeX/fontdata.js

Updates to Questionbank

User interface language: English | Español

Date	May 2014	Marks available	2	Reference code	14M.1.sl.TZ2.3
Level	SL only	Paper	1	Time zone	TZ2
Command term	Find	Question number	3	Adapted from	N/A

Question

The following diagram shows the graph of $y = f(x)$ , for $- 4 \le x \le 5$ .

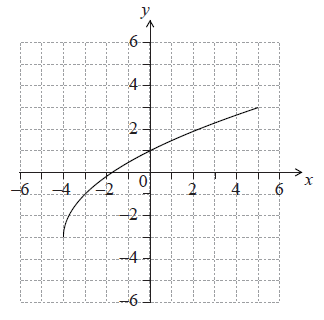
Write down the value of $f( - 3)$ .

[1]

a(i).

${f^{ - 1}}(1)$ .

[1]

a(ii).

Find the domain of ${f^{ - 1}}$ .

[2]

b.

On the grid above, sketch the graph of ${f^{ - 1}}$ .

[3]

c.

Markscheme

$f( - 3) = - 1$ A1 N1

[1 mark]

a(i).

${f^{ - 1}}(1) = 0$ (accept $y = 0$ ) A1 N1

[1 mark]

a(ii).

domain of ${f^{ - 1}}$ is range of \(f\) (R1)

eg ${\text{R}}f = {\text{D}}{f^{ - 1}}$

correct answer A1 N2

eg $- 3 \leqslant x \leqslant 3,{\text{ }}x \in [ - 3,{\text{ }}3]{\text{ (accept }} - 3 < x < 3,{\text{ }} - 3 \leqslant y \leqslant 3)$

[2 marks]

b.

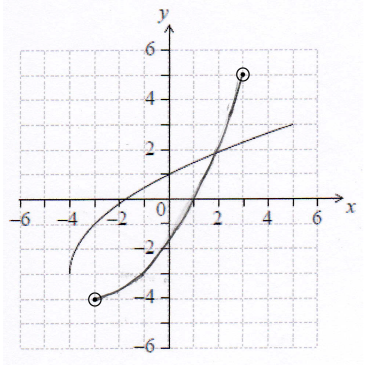A1A1 N2

Note: Graph must be approximately correct reflection in $y = x$ .

Only if the shape is approximately correct, award the following:

A1 for x-intercept at $1$ , and A1 for endpoints within circles.

[2 marks]

c.

Examiners report

[N/A]

a(i).

[N/A]

a(ii).

[N/A]

b.

[N/A]

c.

Syllabus sections

Topic 2 - Functions and equations » 2.1 » Concept of function

$f:x \mapsto f\left( x \right)$ .

Show 22 related questions

17M.2.sl.TZ2.3c: Write down the domain of $g$ .
17M.2.sl.TZ2.3b: On the grid above, sketch the graph of $g$ .
17M.2.sl.TZ2.3a: Write down the range of $f$ .
16M.1.sl.TZ1.1c: Find ${f^{ - 1}}(x)$ .
16M.1.sl.TZ1.1b: Find $(f \circ g)(x)$ .
16M.1.sl.TZ1.1a: Write down $g(2)$ .
08N.1.sl.TZ0.4b: Write down the range of ${f^{ - 1}}$ .
08M.1.sl.TZ2.5b(i) and (ii): Let $g(x) = f(x + 3)$ . (i) Find $g( - 3)$ . (ii) Describe fully the...
09N.1.sl.TZ0.1a: (i) Find $g(0)$ . (ii) Find $(f \circ g)(0)$ .
SPNone.2.sl.TZ0.10a(i), (ii) and (iii): Jane thinks that the function $f(t) = - 0.25{t^3} - 2.32{t^2} + 1.93t + 106$ is a suitable...
13M.1.sl.TZ1.10a: Find the value of $f(0)$ .
13M.2.sl.TZ1.9c: Find the range of $f$ .
13M.2.sl.TZ1.9a: Write down $f(0)$ .
13M.1.sl.TZ2.4a.i: Write down the value of $f(2)$ .
13M.1.sl.TZ2.10c: find the $y$ -coordinate of P.
13M.1.sl.TZ2.10a: Write down the value of $g(3)$ , of $f'(3)$ , and of $h''(2)$ .
14M.1.sl.TZ2.3a(ii): Write down the value of ${f^{ - 1}}(1)$ .
14M.1.sl.TZ2.3a(i): Write down the value of $f( - 3)$ .
17N.1.sl.TZ0.3c: On the grid, sketch the graph of ${f^{ - 1}}$ .
17N.1.sl.TZ0.3b.ii: Write down ${f^{ - 1}}(2)$ .
17N.1.sl.TZ0.3b.i: Write down $f(2)$ ;
17N.1.sl.TZ0.3a: Write down the range of $f$ .

Hide related questions