| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.sl.TZ1.1 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
A discrete random variable \(X\) has the following probability distribution.
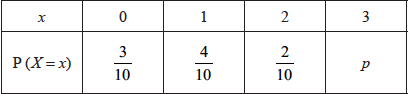
Find \(p\).
Find \({\text{E}}(X)\).
Markscheme
summing probabilities to 1 (M1)
eg,\(\;\;\;\sum { = 1,{\text{ }}3 + 4 + 2 + x = 10} \)
correct working (A1)
\(\frac{3}{{10}} + \frac{4}{{10}} + \frac{2}{{10}} + p = 1,{\text{ }}p = 1 - \frac{9}{{10}}\)
\(p = \frac{1}{{10}}\) A1 N3
[3 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg\(\;\;\;0\left( {\frac{3}{{10}}} \right) + \ldots + 3(p)\)
correct working (A1)
eg\(\;\;\;\frac{4}{{10}} + \frac{4}{{10}} + \frac{3}{{10}}\)
\({\text{E}}(X) = \frac{{11}}{{10}}\;\;\;(1.1)\) A1 N2
[3 marks]
Total [6 marks]
Examiners report
Most candidates were able to find \(p\), however expectation emerged as surprisingly more difficult. Quite often \({\text{E}}(X)/4\) was found or candidates wrote the formula with no further work.
Most candidates were able to find \(p\), however expectation emerged as surprisingly more difficult. Quite often \({\text{E}}(X)/4\) was found or candidates wrote the formula with no further work.

