| Date | None Specimen | Marks available | 8 | Reference code | SPNone.1.sl.TZ0.9 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
Two standard six-sided dice are tossed. A diagram representing the sample space is shown below.
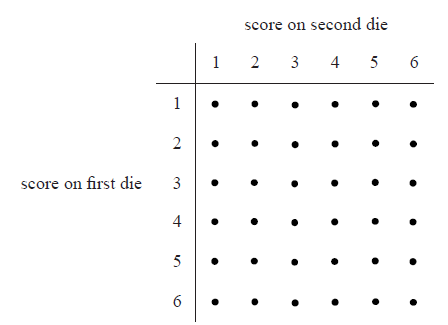
Let \(X\) be the sum of the scores on the two dice.
(i) Find \({\rm{P}}(X = 6)\) .
(ii) Find \({\rm{P}}(X > 6)\) .
(iii) Find \({\rm{P}}(X = 7|X > 6)\) .
Elena plays a game where she tosses two dice.
If the sum is 6, she wins 3 points.
If the sum is greater than 6, she wins 1 point.
If the sum is less than 6, she loses k points.
Find the value of k for which the game is fair.
Markscheme
(i) number of ways of getting \(X = 6\) is 5 A1
\({\rm{P}}(X = 6) = \frac{5}{{36}}\) A1 N2
(ii) number of ways of getting \(X > 6\) is 21 A1
\({\rm{P}}(X > 6) = \frac{{21}}{{36}}\left( { = \frac{7}{{12}}} \right)\) A1 N2
(iii) \({\rm{P}}(X = 7|X > 6) = \frac{6}{{21}}\left( { = \frac{2}{7}} \right)\) A2 N2
[6 marks]
attempt to find \({\rm{P}}(X < 6)\) M1
e.g. \(1 - \frac{5}{{36}} - \frac{{21}}{{36}}\)
\({\rm{P}}(X < 6) = \frac{{10}}{{36}}\) A1
fair game if \({\rm{E}}(W) = 0\) (may be seen anywhere) R1
attempt to substitute into \({\rm{E}}(X)\) formula M1
e.g. \(3\left( {\frac{5}{{36}}} \right) + 1\left( {\frac{{21}}{{36}}} \right) - k\left( {\frac{{10}}{{36}}} \right)\)
correct substitution into \({\rm{E}}(W) = 0\) A1
e.g. \(3\left( {\frac{5}{{36}}} \right) + 1\left( {\frac{{21}}{{36}}} \right) - k\left( {\frac{{10}}{{36}}} \right) = 0\)
work towards solving M1
e.g. \(15 + 21 - 10k = 0\)
\(36 = 10k\) A1
\(k = \frac{{36}}{{10}}( = 3.6)\) A1 N4
[8 marks]

