| Date | November 2014 | Marks available | 5 | Reference code | 14N.1.sl.TZ0.9 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
The following diagram shows the graph of a function \(f\). There is a local minimum point at \(A\), where \(x > 0\).
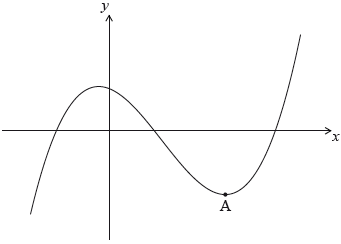
The derivative of \(f\) is given by \(f'(x) = 3{x^2} - 8x - 3\).
Find the \(x\)-coordinate of \(A\).
The \(y\)-intercept of the graph is at (\(0,6\)). Find an expression for \(f(x)\).
The graph of a function \(g\) is obtained by reflecting the graph of \(f\) in the \(y\)-axis, followed by a translation of \(\left({\begin{array}{*{20}{c}}m\\n\end{array}}\right)\).
Find the \(x\)-coordinate of the local minimum point on the graph of \(g\).
Markscheme
recognizing that the local minimum occurs when \(f'(x) = 0\) (M1)
valid attempt to solve \(3{x^2} - 8x - 3 = 0\) (M1)
eg\(\;\;\;\)factorization, formula
correct working A1
\((3x + 1)(x - 3),{\text{ }}x = \frac{{8 \pm \sqrt {64 + 36} }}{6}\)
\(x = 3\) A2 N3
Note: Award A1 if both values \(x = \frac{{ - 1}}{3},{\text{ }}x = 3\) are given.
[5 marks]
valid approach (M1)
\(f(x) = \int {f'(x){\text{d}}x} \)
\(f(x) = {x^3} - 4{x^2} - 3x + c\;\;\;\)(do not penalize for missing “\( + c\)”) A1A1A1
\(c = 6\) (A1)
\(f(x) = {x^3} - 4{x^2} - 3x + 6\) A1 N6
[6 marks]
applying reflection (A1)
eg\(\;\;\;f( - x)\)
recognizing that the minimum is the image of \(A\) (M1)
eg\(\;\;\;x = - 3\)
correct expression for \(x\) A1 N3
eg\(\;\;\; - 3 + m,{\text{ }}\left( {\begin{array}{*{20}{c}} { - 3 + m} \\ { - 12 + n} \end{array}} \right),{\text{ }}(m - 3,{\text{ }}n - 12)\)
[3 marks]
Total [14 marks]
Examiners report
The majority of candidates approached part (a) correctly, and most recognized that only one solution was possible within the given domain.
Nearly all candidates answered part (b) correctly, earning all the available marks for integrating the polynomial and solving for \(C\).
Part (c) proved to be much more difficult for candidates, who either did not know how to apply the transformations correctly, or who engaged in lengthy and unnecessary manipulations of the function, rather than simply finding the image of the local minimum point \(A\).

