| Date | November 2013 | Marks available | 2 | Reference code | 13N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \frac{{{{(\ln x)}^2}}}{2}\), for \(x > 0\).
Let \(g(x) = \frac{1}{x}\). The following diagram shows parts of the graphs of \(f'\) and g.
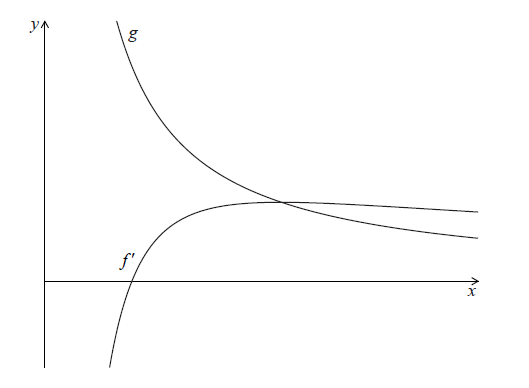
The graph of \(f'\) has an x-intercept at \(x = p\).
Show that \(f'(x) = \frac{{\ln x}}{x}\).
There is a minimum on the graph of \(f\). Find the \(x\)-coordinate of this minimum.
Write down the value of \(p\).
The graph of \(g\) intersects the graph of \(f'\) when \(x = q\).
Find the value of \(q\).
The graph of \(g\) intersects the graph of \(f'\) when \(x = q\).
Let \(R\) be the region enclosed by the graph of \(f'\), the graph of \(g\) and the line \(x = p\).
Show that the area of \(R\) is \(\frac{1}{2}\).
Markscheme
METHOD 1
correct use of chain rule A1A1
eg \(\frac{{2\ln x}}{2} \times \frac{1}{x},{\text{ }}\frac{{2\ln x}}{{2x}}\)
Note: Award A1 for \(\frac{{2\ln x}}{{2x}}\), A1 for \( \times \frac{1}{x}\).
\(f'(x) = \frac{{\ln x}}{x}\) AG N0
[2 marks]
METHOD 2
correct substitution into quotient rule, with derivatives seen A1
eg \(\frac{{2 \times 2\ln x \times \frac{1}{x} - 0 \times {{(\ln x)}^2}}}{4}\)
correct working A1
eg \(\frac{{4\ln x \times \frac{1}{x}}}{4}\)
\(f'(x) = \frac{{\ln x}}{x}\) AG N0
[2 marks]
setting derivative \( = 0\) (M1)
eg \(f'(x) = 0,{\text{ }}\frac{{\ln x}}{x} = 0\)
correct working (A1)
eg \(\ln x = 0,{\text{ }}x = {{\text{e}}^0}\)
\(x = 1\) A1 N2
[3 marks]
intercept when \(f'(x) = 0\) (M1)
\(p = 1\) A1 N2
[2 marks]
equating functions (M1)
eg \(f' = g,{\text{ }}\frac{{\ln x}}{x} = \frac{1}{x}\)
correct working (A1)
eg \(\ln x = 1\)
\(q = {\text{e (accept }}x = {\text{e)}}\) A1 N2
[3 marks]
evidence of integrating and subtracting functions (in any order, seen anywhere) (M1)
eg \(\int_q^e {\left( {\frac{1}{x} - \frac{{\ln x}}{x}} \right){\text{d}}x{\text{, }}\int {f' - g} } \)
correct integration \(\ln x - \frac{{{{(\ln x)}^2}}}{2}\) A2
substituting limits into their integrated function and subtracting (in any order) (M1)
eg \((\ln {\text{e}} - \ln 1) - \left( {\frac{{{{(\ln {\text{e}})}^2}}}{2} - \frac{{{{(\ln 1)}^2}}}{2}} \right)\)
Note: Do not award M1 if the integrated function has only one term.
correct working A1
eg \((1 - 0) - \left( {\frac{1}{2} - 0} \right),{\text{ }}1 - \frac{1}{2}\)
\({\text{area}} = \frac{1}{2}\) AG N0
Notes: Candidates may work with two separate integrals, and only combine them at the end. Award marks in line with the markscheme.
[5 marks]

