| Date | November 2008 | Marks available | 3 | Reference code | 08N.1.sl.TZ0.6 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down, Hence, and Show that | Question number | 6 | Adapted from | N/A |
Question
The diagram shows part of the graph of \(y = f'(x)\) . The x-intercepts are at points A and C. There is a minimum at B, and a maximum at D.
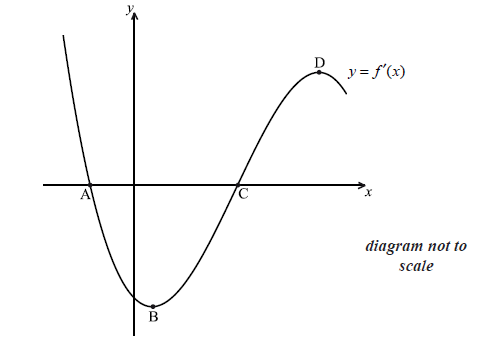
(i) Write down the value of \(f'(x)\) at C.
(ii) Hence, show that C corresponds to a minimum on the graph of f , i.e. it has the same x-coordinate.
Which of the points A, B, D corresponds to a maximum on the graph of f ?
Show that B corresponds to a point of inflexion on the graph of f .
Markscheme
(i) \(f'(x) = 0\) A1 N1
(ii) METHOD 1
\(f'(x) < 0\) to the left of C, \(f'(x) > 0\) to the right of C R1R1 N2
METHOD 2
\(f''(x) > 0\) R2 N2
[3 marks]
A A1 N1
[1 mark]
METHOD 1
\(f''(x) = 0\) R2
discussion of sign change of \(f''(x)\) R1
e.g. \(f''(x) < 0\) to the left of B and \(f''(x) > 0\) to the right of B; \(f''(x)\) changes sign either side of B
B is a point of inflexion AG N0
METHOD 2
B is a minimum on the graph of the derivative \({f'}\) R2
discussion of sign change of \(f''(x)\) R1
e.g. \(f''(x) < 0\) to the left of B and \(f''(x) > 0\) to the right of B; \(f''(x)\) changes sign either side of B
B is a point of inflexion AG N0
[3 marks]
Examiners report
The variation in successful and unsuccessful responses to this question was remarkable. Many candidates did not even attempt it. Candidates could often determine from the graph, the minimum and maximum values of the original function, but few could correctly use the graph to analyse and justify these results. Responses indicated that some candidates did not realize that they were looking at the graph of \({f'}\) and not the graph of \(f\) .
The variation in successful and unsuccessful responses to this question was remarkable. Many candidates did not even attempt it. Candidates could often determine from the graph, the minimum and maximum values of the original function, but few could correctly use the graph to analyse and justify these results. Responses indicated that some candidates did not realize that they were looking at the graph of \({f'}\) and not the graph of \(f\) .
In part (c), many candidates once more failed to respect the command term "show" and often provided an incomplete answer. Candidates should be encouraged to refer to the number of marks available for a particular part when deciding how much information should be given.

