| Date | May 2008 | Marks available | 4 | Reference code | 08M.2.sl.TZ2.9 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Write down | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = {{\rm{e}}^x}(1 - {x^2})\) .
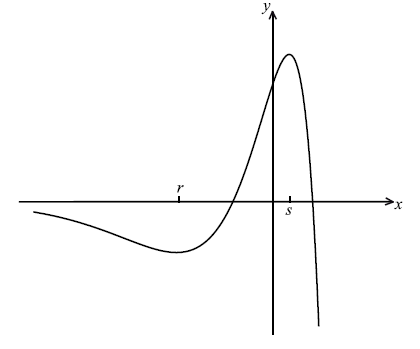
Part of the graph of \(y = f(x)\), for \( - 6 \le x \le 2\) , is shown below. The x-coordinates of the local minimum and maximum points are r and s respectively.
Show that \(f'(x) = {{\rm{e}}^x}(1 - 2x - {x^2})\) .
Write down the equation of the horizontal asymptote.
Write down the value of r and of s.
Let L be the normal to the curve of f at \({\text{P}}(0{\text{, }}1)\) . Show that L has equation \(x + y = 1\) .
Let R be the region enclosed by the curve \(y = f(x)\) and the line L.
(i) Find an expression for the area of R.
(ii) Calculate the area of R.
Markscheme
evidence of using the product rule M1
\(f'(x) = {{\rm{e}}^x}(1 - {x^2}) + {{\rm{e}}^x}( - 2x)\) A1A1
Note: Award A1 for \({{\rm{e}}^x}(1 - {x^2})\) , A1 for \({{\rm{e}}^x}( - 2x)\) .
\(f'(x) = {{\rm{e}}^x}(1 - 2x - {x^2})\) AG N0
[3 marks]
\(y = 0\) A1 N1
[1 mark]
at the local maximum or minimum point
\(f'(x) = 0\) \(({{\rm{e}}^x}(1 - 2x - {x^2}) = 0)\) (M1)
\( \Rightarrow 1 - 2x - {x^2} = 0\) (M1)
\(r = - 2.41\) \(s = 0.414\) A1A1 N2N2
[4 marks]
\(f'(0) = 1\) A1
gradient of the normal \(= - 1\) A1
evidence of substituting into an equation for a straight line (M1)
correct substitution A1
e.g. \(y - 1 = - 1(x - 0)\) , \(y - 1 = - x\) , \(y = - x + 1\)
\(x + y = 1\) AG N0
[4 marks]
(i) intersection points at \(x = 0\) and \(x = 1\) (may be seen as the limits) (A1)
approach involving subtraction and integrals (M1)
fully correct expression A2 N4
e.g. \(\int_0^1 {\left( {{{\rm{e}}^x}(1 - {x^2}) - (1 - x)} \right)} {\rm{d}}x\) , \(\int_0^1 {f(x){\rm{d}}x - \int_0^1 {(1 - x){\rm{d}}x} } \)
(ii) area \(R = 0.5\) A1 N1
[5 marks]
Examiners report
Many candidates clearly applied the product rule to correctly show the given derivative. Some candidates missed the multiplicative nature of the function and attempted to apply a chain rule instead.
For part (b), the equation of the horizontal asymptote was commonly written as \(x = 0\) .
Although part (c) was a “write down” question where no working is required, a good number of candidates used an algebraic method of solving for r and s which sometimes returned incorrect answers. Those who used their GDC usually found correct values, although not always to three significant figures.
In part (d), many candidates showed some skill showing the equation of a normal, although some tried to work with the gradient of the tangent.
Surprisingly few candidates set up a completely correct expression for the area between curves that considered both integration and the correct subtraction of functions. Using limits of \( - 6\) and 2 was a common error, as was integrating on \(f(x)\) alone. Where candidates did write a correct expression, many attempted to perform analytic techniques to calculate the area instead of using their GDC.

