| Date | May 2009 | Marks available | 4 | Reference code | 09M.2.sl.TZ2.8 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
Let \(f(x) = x{(x - 5)^2}\) , for \(0 \le x \le 6\) . The following diagram shows the graph of f .
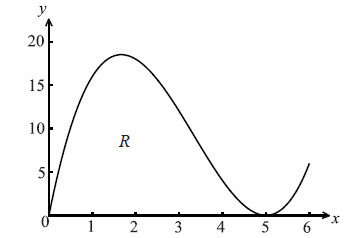
Let R be the region enclosed by the x-axis and the curve of f .
Find the area of R.
Find the volume of the solid formed when R is rotated through \({360^ \circ }\) about the x-axis.
The diagram below shows a part of the graph of a quadratic function \(g(x) = x(a - x)\) . The graph of g crosses the x-axis when \(x = a\) .
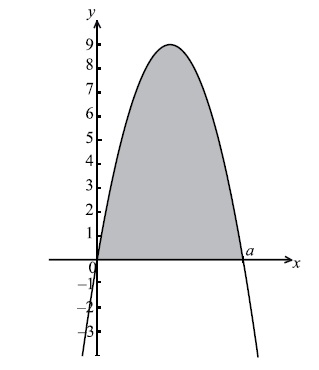
The area of the shaded region is equal to the area of R. Find the value of a.
Markscheme
finding the limits \(x = 0\) , \(x = 5\) (A1)
integral expression A1
e.g. \(\int_0^5 {f(x){\rm{d}}x} \)
area = 52.1 A1 N2
[3 marks]
evidence of using formula \(v = \int {\pi {y^2}{\rm{d}}x} \) (M1)
correct expression A1
e.g. volume \( = \pi \int_0^5 {{x^2}{{(x - 5)}^4}{\rm{d}}x} \)
volume = 2340 A2 N2
[4 marks]
area is \(\int_0^a {x(a - x){\rm{d}}x} \) A1
\( = \left[ {\frac{{a{x^2}}}{2} - \frac{{{x^3}}}{3}} \right]_0^a\) A1A1
substituting limits (M1)
e.g. \(\frac{{{a^3}}}{2} - \frac{{{a^3}}}{3}\)
setting expression equal to area of R (M1)
correct equation A1
e.g. \(\frac{{{a^3}}}{2} - \frac{{{a^3}}}{3} = 52.1\) , \({a^3} = 6 \times 52.1\)
\(a = 6.79\) A1 N3
[7 marks]
Examiners report
Many candidates set up a completely correct equation for the area enclosed by the x-axis and the curve. Also, many of them tried an analytic approach which sometimes returned incorrect answers. Using the wrong limits \(0\) and \(6\) was a common error.
The formula for the volume of revolution given in the data booklet was seen many times in part (b). Some candidates wrote the integrand incorrectly, either missing the \(\pi \) or not squaring. A good number of students could write a completely correct integral expression for the volume of revolution but fewer could evaluate it correctly as many started an analytical approach instead of using their GDC.
Many candidates did not use a GDC at all in this question. Pages of calculations were produced in an effort to find the area and the volume of revolution. This probably caused a shortage of time for later questions.
Many candidates did not use a GDC at all in this question. Pages of calculations were produced in an effort to find the area and the volume of revolution. This probably caused a shortage of time for later questions.

