| Date | November 2008 | Marks available | 4 | Reference code | 08N.2.sl.TZ0.4 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Let \(f(x) = x\cos (x - \sin x)\) , \(0 \le x \le 3\) .
Sketch the graph of f on the following set of axes.
The graph of f intersects the x-axis when \(x = a\) , \(a \ne 0\) . Write down the value of a.
The graph of f is revolved \(360^\circ \) about the x-axis from \(x = 0\) to \(x = a\) . Find the volume of the solid formed.
Markscheme
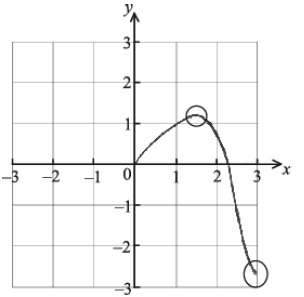 A1A2 N3
A1A2 N3
Notes: Award A1 for correct domain, \(0 \le x \le 3\) . Award A2 for approximately correct shape, with local maximum in circle 1 and right endpoint in circle 2.
[3 marks]
\(a = 2.31\) A1 N1
[1 mark]
evidence of using \(V = \pi {\int {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) (M1)
fully correct integral expression A2
e.g. \(V = \pi {\int_0^{2.31} {\left[ {x\cos (x - \sin x)} \right]} ^2}{\rm{d}}x\) , \(V = \pi {\int_0^{2.31} {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) A1 N2
\(V = 5.90\)
[4 marks]
Examiners report
Many candidates sketched a clear and smooth freehand curve with the local maximum, x-intercept and endpoints in approximately correct positions. Commonly, candidates sketched a graph across \([ - 3{\text{, }}3]\) , which neglects the given domain of the function. There were some candidates who sketched a straight line through the origin, presumably from being in the degree mode of their GDC.
Many candidates sketched a clear and smooth freehand curve with the local maximum, x-intercept and endpoints in approximately correct positions. Commonly, candidates sketched a graph across \([ - 3{\text{, }}3]\) , which neglects the given domain of the function. There were some candidates who sketched a straight line through the origin, presumably from being in the degree mode of their GDC.
A good number of candidates could set up the correct integral expression for volume, but surprisingly few were able to use their GDC to find the correct value. Some attempted to analytically integrate the square of this unusual function, expending valuable time in this effort. A small but significant number of candidates wrote a final answer as \(1.88\pi \) , which accrued the accuracy penalty.

