| Date | November 2016 | Marks available | 3 | Reference code | 16N.2.sl.TZ0.6 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | How long | Question number | 6 | Adapted from | N/A |
Question
All lengths in this question are in metres.
Let \(f(x) = - 0.8{x^2} + 0.5\), for \( - 0.5 \leqslant x \leqslant 0.5\). Mark uses \(f(x)\) as a model to create a barrel. The region enclosed by the graph of \(f\), the \(x\)-axis, the line \(x = - 0.5\) and the line \(x = 0.5\) is rotated 360° about the \(x\)-axis. This is shown in the following diagram.
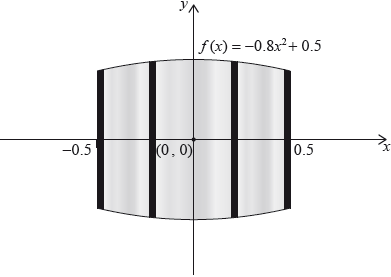
Use the model to find the volume of the barrel.
The empty barrel is being filled with water. The volume \(V{\text{ }}{{\text{m}}^3}\) of water in the barrel after \(t\) minutes is given by \(V = 0.8(1 - {{\text{e}}^{ - 0.1t}})\). How long will it take for the barrel to be half-full?
Markscheme
attempt to substitute correct limits or the function into the formula involving
\({y^2}\)
eg\(\,\,\,\,\,\)\(\pi \int_{ - 0.5}^{0.5} {{y^2}{\text{d}}x,{\text{ }}\pi \int {{{( - 0.8{x^2} + 0.5)}^2}{\text{d}}x} } \)
0.601091
volume \( = 0.601{\text{ }}({{\text{m}}^3})\) A2 N3
[3 marks]
attempt to equate half their volume to \(V\) (M1)
eg\(\,\,\,\,\,\)\(0.30055 = 0.8(1 - {{\text{e}}^{ - 0.1t}})\), graph
4.71104
4.71 (minutes) A2 N3
[3 marks]

