| Date | November 2012 | Marks available | 2 | Reference code | 12N.1.sl.TZ0.4 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Part of the graph of \(f(x) = a{x^3} - 6{x^2}\) is shown below.
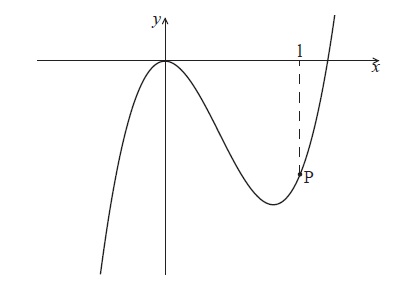
The point P lies on the graph of \(f\) . At P, x = 1.
Find \(f'(x)\) .
The graph of \(f\) has a gradient of \(3\) at the point P. Find the value of \(a\) .
Markscheme
\(f'(x) = 3a{x^2} - 12x\) A1A1 N2
Note: Award A1 for each correct term.
[2 marks]
setting their derivative equal to 3 (seen anywhere) A1
e.g. \(f'(x) = 3\)
attempt to substitute \(x = 1\) into \(f'(x)\) (M1)
e.g. \(3a{(1)^2} - 12(1)\)
correct substitution into \(f'(x)\) (A1)
e.g. \(3a - 12\) , \(3a = 15\)
\(a = 5\) A1 N2
[4 marks]
Examiners report
A majority of candidates answered part (a) correctly, and a good number earned full marks on both parts of this question. In part (b), some common errors included setting the derivative equal to zero, or substituting 3 for x in their derivative. There were also a few candidates who incorrectly tried to work with \(f(x)\) , rather than \(f'(x)\) , in part (b).
A majority of candidates answered part (a) correctly, and a good number earned full marks on both parts of this question. In part (b), some common errors included setting the derivative equal to zero, or substituting \(3\) for \(x\) in their derivative. There were also a few candidates who incorrectly tried to work with \(f(x)\) , rather than \(f'(x)\) , in part (b).

